Idle Cell Life.

In this essay, Idle Theory sets out to construct a simple model of a cell which outlines how cells acquire and expend energy, and how they can grow and reproduce and die.

Biology has no succinct, unambiguous definition of life. Instead it offers a set of the principal characteristics of life. These vary from text to text, but the common characteristics of living creatures seems to be that:

a) they are composed of cells,
b) the cells grow,
c) the cells reproduce by dividing in two,
d) the cells acquire and expend energy ( metabolise ),
e) the cells contain DNA.
f) the cells also die.

The Idle Primitive:

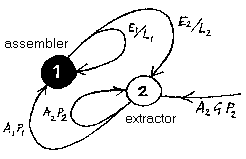
In Idle Theory, while the actualities of cells are kept in mind, an abstract cell model is constructed. The ribosomes which produce proteins are replaced by 'assemblers' which require energy to build cell components. The assemblers are supplied with energy by 'extractors' which induct energy from the external environment. Both assemblers and extractors are either active or inactive, and when active they use energy at a constant rate. Chemical energy inducted by the extractors powers both extractors and assemblers. Both assemblers and extractors have limited lifetimes after which they are assumed to disintegrate. The assemblers are able to construct both assemblers and extractors. In this model, assemblers cannot operate unless supplied by extractors. And extractors cannot operate unless maintained or replaced by assemblers. The pairing of one extractor with one assembler is called a "primitive," and cells are regarded as made up of a number of primitives.

Cell processes can be thought of as transducers which convert an input into an output. The process may be thought of as chemical process where A + B -> C + D, but also as a factory which use energy to transform raw material, a, into product, b.

These processes can be chained together, so that the output of one is the input, or one of the inputs, of another process. The factory can make products which form the raw material input to another factory.

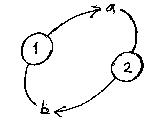
Living creatures maintain themselves, and their production processes are looped back round on themselves. For example, ribosomes link amino acids together to form proteins. Some of these proteins then induct amino acids from the external environment to the ribosomes production sites.

To continue the factory analogy, a factory might make trucks from steel, rubber, and plastic. If these trucks could then transport steel, plastic, rubber, etc, to the factory, and feed its production, then truck and factory are looped round.

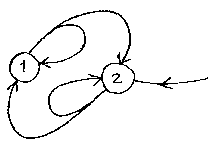
In principle, a self-feeding looped set of processes should be able to continue indefinitely. In reality, there are always inefficiencies and losses which require the loop to be continually supplied with energy if its component processes are to keep running.

The Idle Life primitive is one of these loops. Component 1 is an assembler which is able to construct assemblers and extractors. Component 2 is an extractor which inducts energy from the external environment. Both components 1 and 2 have limited lifetimes, after which they disintegrate. And both components are either active or inactive, and when active - making components, sucking in fuel - they each use energy at a constant rate. Thus to simply maintain the number of components, the assembler has to keep making just enough new components to offset the losses as the components reach the end of their lives. And the extractor has to work hard enough to supply enough fuel to power both the assembler and its own energy demands.

Expressed in energy terms, component 1 - the assembler - is assumed to have an energy cost of production E₁, and a lifetime L₁. Similarly, component 2 - the extractor - is assumed to have an energy cost of production E₂ and a lifetime L₂. The rate of energy expenditure, or power consumption, of the assembler in making component 1 is then E₁/L₁, and the power consumption in making component 2 is E₂/L₂. If the power consumption of the assembler is P₁ while it is actively assembling components, and zero while idle, then if the assembler needs to be active for A₁ of the time to meet its production targets then:

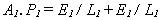
Process 2 - the extractor - similarly has a power consumption P₂ while it is pumping fuel into the primitive, and is active for A₂ of the time. The power input to the primitive while the extractor is pumping fuel is some multiple, G, of its power consumption. G reflects the abundance of energy in the external environment. An energy-rich environment results in a high value of G. If G was as low as 1, then the extractor would expend one unit of energy to acquire one unit of energy, and be unable to supply the assembler with any energy to drive its production. Thus G must be greater than unity, and the energy content of fuel extracted from the environment must be greater than the energy cost of extraction. At equilibrium, when the power input from the external environment equals the power expenditure of processes 1 and 2:

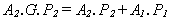
In the equilibrium state, the primitive - component 1 and 2 - neither grows nor contracts. Since both processes alternate in time between active/busy and inactive/ idle states, A1 and A2 are the fraction of time that these processes are busy. The Idleness, I, of any process is then simply 1 - A, where I = 0 means continuous activity and I = 1 means continuous inactivity. Where I₁ is assembler idleness, and I₂ is extractor idleness:

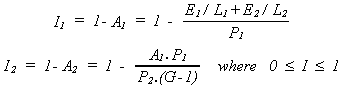
and the power consumption - metabolic rate - of the primitive is A₂.G.P₂.

At equilibrium, just maintaining itself, the primitive has an excess unused power capacity of I₂.G.P₂. At equilibrium, the extractor is idle for a fraction I of its cycle time. If, instead of being idle, it was active, I₂.G.P₂ is the maximum power available to the primitive to drive other processes.

The extractor gain, G, may appear to be a case of getting something for nothing. But all it reflects is the possibility that the energy cost of physically transporting fuel - for example, glucose and oxygen - into the primitive may be less than the energy released when glucose and oxygen combine to produce carbon dioxide and water.

Primitive death:

The primitive disintegrates - dies - if equilibrium idleness of either assembler or extractor falls to zero, or if the primitive operates at a higher idleness than equilibrium idleness. In the first case, the primitive becomes unable, working continuously, to supply enough fuel or make enough replacement components to maintain itself. In the second case, the primitive is does not work long enough to meet its maintenance requirements.

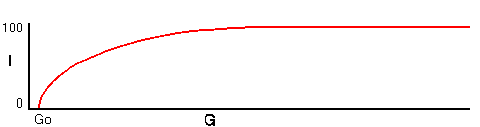
The characteristic curve of extractor idleness as the extractor gain, G, falls is one where idleness approaches unity at high values of G - when the environment is energy-rich -, and falls off increasingly rapidly as G falls, with idleness reaching zero when G is some value G₀. As G falls below G₀ idleness remains at zero. Assembler idleness varies with component lifetime in a similar way.

1) The primitive can continue operating - survive - given favourable values of E, L, P₁, P₂, and G. If the lifetime of components falls, because the environment is hot, acidic, or hostile in some other way, I₁ decreases as the assembler has to work longer producing replacements, and I₂ also falls as the extractor has to supply more energy to the busy assembler. Equally, if fuel energy density in the surrounding environment falls, G will fall, as the extractor pumps in less energy for the same energy expenditure, and I₂ will fall. In a deteriorating environment, falling extractor idleness reaches a limit where either I₂ reaches zero. Past this point, the extractor is unable to maintain fuel levels. If the fuel store is minimal, the excess of fuel consumption over replacement will rapidly result in fuel store exhaustion, and both extractor and assembler will cease operating, and the primitive will disintegrate. This is the zero idleness 'death', ZID, of the primitive. In subsequent discussions, it is taken that ZID occurs immediately when either extractor or assembler idleness reaches zero.

2) The primitive can also die if it allows assembler or extractor idleness to rise above their equilibrium levels. In this case, either the extractor does not pump in enough fuel, or the assembler does not make enough new components. Either way, the primitive fails to maintain itself, and disintegrates.

Non-equilibrium primitives:

At equilibrium, the two components of the primitive perform just enough work to maintain the primitive. The assembler makes a new extractor and assembler just in time to replace the last ones, as they reach the end of their lives.

But this equilibrium state need not be supposed to be the normal state for a primitive. The components of the primitive may perform more work or less work than is required for equilibrium.

If the primitive operates at less than equilibrium idleness, doing more work than is required to just maintain itself, it produces fuel and components at a greater rate than are required, and the number of components increases. If an assembler produces replacement components faster than these components are used up, then the number of components will gradually increase. After a while there will be 2 assemblers and 2 extractors, then 3, 4, and so on. Assuming that assemblers overproduces components in the same constant proportion, the result is exponential reproduction.

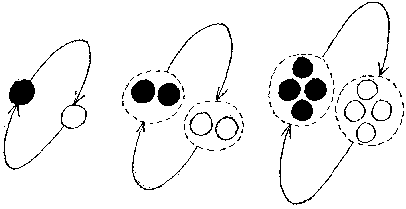
The other alternative is that a primitive operates at above equilibrium idleness, doing less work than is required to just maintain itself. In this circumstance, when an assembler or extractor reaches the end of its working life, its replacement isn't complete. If an extractor is not replaced, no further energy is extracted from the environment, and the remaining assembler rapidly runs out of fuel to power it. If it is the assembler which is not replaced, then no further assemblers or extractors are produced, even though fuel is present to power these activities. If, through overproduction, primitives multiply in numbers, then underproduction results in a decrease in numbers, that ultimately reaches zero.

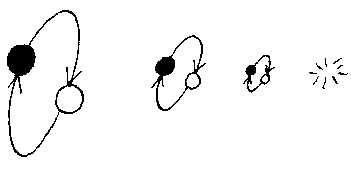
Given some population of separate primitives, some of which undermaintain themselves, and some of which overmaintain themselves, and some exactly maintain themselves, the undermaintainers will all dwindle away and vanish, leaving only overmaintainers and exact maintainers.

Exact self-maintenance is a knife-edge point. The probability of a primitive managing to exactly maintain itself is very small. It is much more likely that it will overmaintain itself to some greater or lesser degree.

Where assemblers overproduce replacement components, the extra production can be denoted by an extra term, P_r, in the extractor idleness equation. P_m is assembler maintenance power consumption, at which it just manages to maintain the assembler and extractor.

Cells as populations of primitives:

Given that the primitives most likely to survive are those which overmaintain themselves, doing a bit more work than is necessary to just maintain themselves, the question then is what happens to these multiplying primitives.

The multiplying primitives may simply disperse. If, however, they adhere together, they may form a variety of geometric configurations - sheets, tubes, spheres. Whichever way, they must organize themselves so that the energy-acquiring extractors form a surface layer at the external environment, with the component-producing assemblers inside.

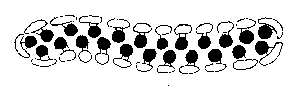
In a community, there may be advantages if components and fuel are pooled, rather than each extractor-assembler pair looking after itself. While one primitive may be unable to induct sufficient fuel, another may have a superabundance, and the converse at another time: pooling resources is a form of insurance. Also if environmental energy density falls and extractors have to work longer, a cell may be able to make relatively more extractors, and thus reduce extractor idleness, while increasing assembler idleness.

If the primitives linked together to form spherical cells with an outer shell of extractors and an inner core of assemblers, a cell would consist of one or more primitives, with a central core of assemblers surrounded by a shell of skin of extractors.

As the population of primitives grew, the population of assemblers would act effectively as a single assembler maintaining the surface population of extractors, without any need for each primitive extractor to remain associated with its original assembler.

The resultant growing spherical cell might just get bigger and bigger. But there are mechanical reasons for supposing that a number of other events could take place.

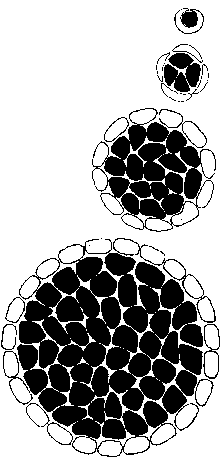
At the outset, with a single primitive, the single extractor would be wrapped around the single assembler. With a doubling of numbers, two extractors would be wrapped around two assemblers, and so on. The growing cell then consists of a surface of N extractors on a sphere whose volume is N assemblers. The volume and surface area of a sphere are :

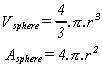
If it is assumed, for simplicity, that the assembler and the extractor have the same unit volume - a cube of unit side length -, and some degree of elasticity, then the surface area of the sphere is equal to the volume when r = 3 and N = 113. Below this value, the surface area of the sphere is greater than the volume. Above this value, the surface area is less than the volume.

Thus when N = 33, for example, the volume of assemblers is 33, and the surface area of the sphere of is 50. Since there are 33 extractors of unit area covering this sphere, these extractors have to be stretched to cover the assembler sphere surface. Thus the extractors must be in tension, and the assembler core is subject to compression.

At N = 113, the surface area of the assembler sphere is 113, and 113 extractors just covers it, and the extractor shell is not in tension.

Above N = 113, the surface area of the assembler core is less than the volume, and the extractor shell becomes increasingly compressed, and the assembler core tensed.

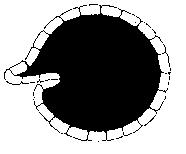
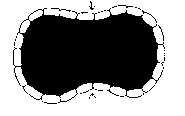
The significance of this is that up to N = 113, the cell has a tensed skin of extractors stretched over a compressed core of assemblers, and will adopt a spherical shape. Above this value, either the cell will try to induct material to increase its core volume so that the surface area matches the area of the extractor skin, or the compressed skin will try to buckle or crumple, as it tries to reach an equilibrium state where it is no longer compressed.

Depending on the characteristics of the assembler skin, this buckling can take many forms. If the skin is capable of bearing compression, it may retain its shape, and vacuoles form in the cell core to act to increase the core volume (as occurs in plant cells), and hence its surface area, and reduce extractor shell compression. Here core volume is increased to reduce skin compression.

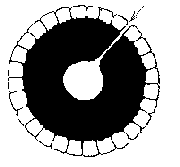
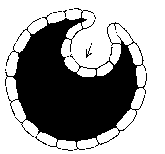
The other option is to reduce the extractor shell area by buckling or crumpling until the extractor skin covers the core. The extractor skin may crumple locally. Or the entire skin may gradually move, as the cell grows, towards a concave sphere, or the surface may buckle into the core of the cell, forming a bubble of extractors within the body of the cell.

In the last case, the internally inducted extractors become unable to acquire energy from the environment, and the remaining extractors decrease in idleness as they work longer to make up the loss.

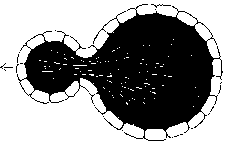
A further possibility is for the cell to bud off a sub-cell from its surface. At N = 226, the 2 resulting cells are of equal size. At lesser values, the 2 cells are of different sizes, with unequal numbers of extractors and assemblers, and unequal extractor idleness and assembler idleness.

Cells with tensed surfaces will not divide, deform, crumple, or induct parts of their surface.

Cell division, in this account, is purely mechanical. This can be explored further.

Control:

Something needs to be said about the control mechanisms that determine the rate and proportions in which components are made, and at which fuel energy is extracted from the environment.

One simple control mechanism that is for the extractors to become active when fuel levels are low (and inactive when they are high), and for assemblers to become active when fuel levels are high (and inactive when low).

It is, however, important that the cell attempts to ensure that all components operate at approximately the same degree of idleness. If, for example, there are many extractors and few assemblers, the assemblers will have to be more busy than the extractors. The danger of inequality is that with an environmental deterioration the assemblers will arrive at zero idleness while the extractors are relatively inactive, and too few extractors and assemblers are made, and the entire system collapses. If the numbers of components in the various processes can be adjusted so that all processes operate at equal idleness, this danger can be minimized.

Biological cell ribosomes are general purpose manufacturers which can use different DNA instructions sequences to build different proteins. If the primitive's assembler is taken to work in the same way. One way of getting the proportions of extractors, assemblers (and any other components) right, and therefore their idleness equal, is for each assembler to work from a set of instructions (much like biological cell ribosomes work from the instructions encoded in mRNA). Each assembler has a loop of multiple instructions which it executes one by one, going round and round the loop. Some of the instructions in the loop code for making assemblers, and some for extractors, and quite possibly various other things as well. If just one extractor is needed for every assembler made, the loop has one set of extractor-making code (an extractor 'gene') and one set of assembler-making code. If the proportion is 2:1, then the loop contains 2 extractor genes, and 1 assembler gene. If the proportion is 256:177, then the loop has 256 extractor genes and 177 assembler genes, and so on. This may make the loop of instructions rather long, but it will be accurate.

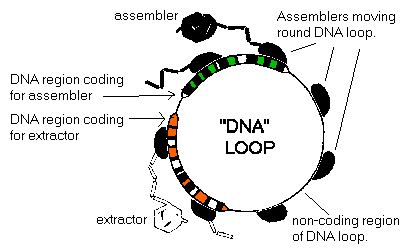
Given such a loop containing multiple genes for the different components of the cell, the assembler will always be busy making either extractors or assemblers. And always busy is probably too busy. So some way has to be found to slow down assembler production, and make the assembler more idle. The way this can be done is to have non-coding 'Do nothing' regions in the instruction loop. Thus, as an assembler chugs steadily round the loop, it is either producing assemblers or extractors as it passes over the genes that code for them, or is produces nothing at all as it executes 'Do nothing' instructions. Where assemblers have to keep busy, there will be little or any non-coding genes. Where assemblers are very idle, 90% or more of the instruction loop will consist of non-coding regions.

Given that these control loops can be very long, and each assembler must have access to one, it makes sense for there to be one single loop of instructions to which all the assemblers have access, each occupying a different site, and all moving in the same direction along it, at the same speed. If the assemblers are evenly distributed along its length, the production of rarely used, but necessary components is ensured.

With such a control loop, made up of finite steps, it may never be possible to get exactly the right proportions and production rates, but only near approximations.

This control loop would have to be adjustable. Thus, if extractor idleness fell, more extractor genes would have to be added into the loop. If extractor idleness fell, they would be removed. If the entire cell's activity rate needed to be raised, non-coding regions would be removed, and vice versa if cell activity was to be reduced. This might not necessarily require the production and destruction of genes, lengthening and shortening the loop. Instead, genes that were not needed would be infolded into the loop, and not executed, because no assembler would reach them.

Since the assemblers and extractors have finite lifespans, and need to be regularly reproduced, the same must apply to the control loop. This is a bit tricky, because as a copy of the loop is in produced, there is a danger that the carefully controlled proportions will all be thrown out of balance, as new sequences are produced, unless the loop can be replicated at one step.

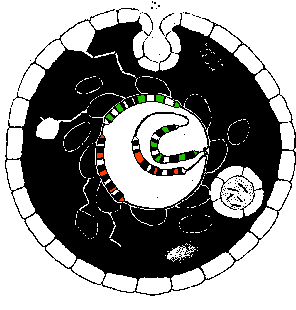
The completed cell, on this model, has a central loop of control code, to which the assemblers are attached, and is surrounded by a shell or skin of extractors. Beyond a certain size, it can be expected to deform, buckle, and induct material in membrane bound packages. And it can also be expected to periodically divide in two.

At division, assuming equal sized sub-cells are formed, each sub-cell can be expected to contain half the contents of the original cell. That is, half of its population of assemblers and extractors, half of its fuel and raw material, and half of its control loops. If, at division, a cell contains only one control loop, it will either go to one sub-cell or the other, or even be torn apart. With no control loop, or half of one, production will be chaotic.

Cell Primitives and Biological Cells:

The theoretical, primitive 'cell' is not a biological cell, but it has many similarities with biological cells. Biological cells are, of course, far more complex. However, prokaryote cells - bacteria - do have loops of DNA. Eukaryote cells found in multicellular plants and animals do not. In prokaryote cells there is some 'junk' DNA which does not code for any proteins. Eukaryote cells frequently have a great deal of this non-coding DNA. From the point of view of Idle theory, this suggests that bacteria are not very idle, and that eukaryotes are more idle.

But the attempt here is not to make any contribution to cell biology, but to construct a model of a living entity that displays the characteristics of life set out at the outset of this chapter. These theoretical 'cells' seem able to do this.

a) they grow, because they tend to 'overmaintain' themselves, producing a growing population of primitives.

b) they reproduce, by division, when their geometry permits or enforces it.

c) they acquire and expend energy ( metabolise ),

e) the cells employ instruction sequences to define and control component construction, and these sequences correspond with biological DNA.

f) they die, by disintegrating, when any of their component processes reaches zero idleness.

Additional processes:

The simple cell model, with two processes, could be expanded to include other processes. If, for example, cells are subjected to compressive forces, a gene that codes for compression-bearing components would prevent disintegration, as would tension-resisting components when the cell is subject to tensile forces.

Variation:

With a control loop of 'genes' determining what the assemblers produce, and at what rate, and what proportion, the replication of the control loop prior to division, with one copy going to each daughter cell, the two daughters would inherit the same characteristics as the mother.

But it is of course perfectly possible that the control loop could be mis-copied, with duplications, changes, pieces subtracted. The cell might also acquire complete new designs for assemblers, extractors, and anything else that gets constructed within the cell. The resultant offspring would then inherit the new genes, and behave accordingly. Mostly the random changes would result in cells which were not viable, but occasionally changes would produce improvements: varieties of extractors which pumped in fuel more efficiently, and so on.

If variation is rapid, then every division could produce a new variant. If it only happens occasionally, a multiplying population of cells would be largely made up of exact replicas of each other, or of a few sub-populations of variant types.