Spinning Chains

Artificial gravity can be generated by spinning a circular space station. In this case, centripetal forces hold masses against the rim of the rotating station.

A spinning chain can be simulated using a number of masses connected by massless ties. These chains behave in interesting ways. When the chains are relatively highly elastic, the spinning chain radius oscillates between a maximum where kinetic energy approaches zero, and a minimum where potential energy stored in the ties approaches zero. The system exchanges kinetic energy for potential energy, much like a pendulum. As the chain contracts, its spins faster. And as it expands, it spins slower.

These chains begin as circular, but appear to become non-circular after several oscillations, sometimes briefly forming approximations of regular polygons, before ultimately becoming chaotic.

Most of these oscillations vanish, or are minimized, when the ties are relatively inelastic or rigid. Such chains appear to maintain their circularity indefinitely.

Fountain

Given such artificial gravity, one interesting question is how a fountain (and a pendulum as well) might behave on a spinning space station.

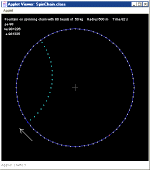
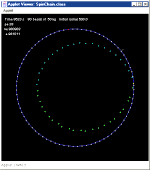
The simulation model of this uses a rigid rotating chain, and fires off a stream of small masses in some direction. It appears that the fountain stream deflects in the direction of rotation of the chain, the opposite of the upward flowing siphon. It is possible to arrange for the fountain to perform a loop back on itself. And also for the fountain to perform several loops.

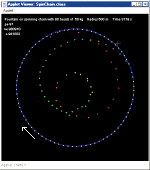The direction and velocity of this stream can be changed by clicking the cursor to give the fountain a new target. The fountain droplets change colour ( cyan -> green -> yellow -> orange -> red -> purple -> blue ) as they 'age'. This helps understanding what is going on in complex configurations. Droplets do not have exactly the same speed and direction in this simulation, because the chain from which they are launched is vibrating as earlier described. Also, since the gravitational forces on all masses, droplets included, is simulated, droplets may occasionally interact with each other.

As part of the spinning chain study, the applet shows chain kinetic energy, k.e., and the potential energy stored in the ties, p.e., and the sum of the two, e. This sum stays roughly constant.

Ties are shown in blue when in tension, and in red when in compression. Since the configuration shown is a high speed, low tension system, oscillations along the chain occasionally result in ties becoming compressed, which shows as a brief red flesh on the chain.

The fountain pump is marked in blue. The red bead is bead 0.

To stop the simulation, move the cursor over the applet. To restart, move the cursor off the applet.

One simple way of understanding what is happening here is to regard each droplet as continuing at some velocity in a straight line. If the hour hand of a clock marks the position of the fountain source on the chain, with the direction of droplets towards the opposite side of the clock, then at 6 o'clock a droplet leaves the fountain heading towards 12 o'clock, and at 7 o'clock a droplet leaves the fountain heading for 1 o'clock, and at 8 o'clock a droplet leaves the fountain for 2 o'clock, and so on. The resulting stream of droplets is 'turning' along its length anticlockwise, although each droplet continues in a straight line. And this is simply the result of the fountain having moved round to point in a slightly different direction. Eventually the droplets reach the other side, by which time the fountain may have revolved all the way round to meet it, and it appears that the fountain stream returns to its source.

To show that the droplets are moving in straight lines, click on the blue square at top right. When it turns red the applet displays the motion trails of all bodies, and the droplets can be seen to be moving in straight lines. Click the red square to turn blue, and return to normal display mode.