JBIS draft

ORBITAL SIPHON OPERATION

Numerical Simulation Model Considerations

The first 2D orbital siphon simulation model began as a static radial chain of masses tied together by massless cables, the motion of which over small intervals of time was calculated using the laws of motion, Newton's law of gravity, and Hooke's law. The model was initialised as a stationary radial tower with some 25 masses connected by equal length elastic ties along a 250,000 km radius chain. The chain was then released at the base and allowed to pull up masses from the equator of the Earth. At this point the first problem was encountered, which was that the rising chain deflected from radial, and stopped pulling up new payload masses from the base, and either reeled back down or entirely collapsed.

The solution to this problem was to constrain the rising chain to a radial path by simply restricting tangential velocities to the angular velocity of the Earth (but without stating how this might practically be done). With this modification in place, the simulation showed that a rising chain would keep pulling up masses from the base, while releasing them from the top. However, here a second problem presented itself, which was that the rising chain tended to accelerate, pulling up masses faster and faster.

The solution to this second problem was to constrain the lowest mass in the rising chain to some peak radial velocity, using some form of braking system (but without specifying what). With these two modifications in place, the principal problem became that of strong radial oscillations within the rising chain. In part these came from the application of the brakes on the lowest body, the lifting of new masses onto the chain at the base, and to a smaller extent the release of masses from the top of the chain.

The solution to these further problems where, firstly, to ensure that the chain accelerated slowly up to operating speed so that the application of the brakes only caused a slight decceleration, secondly, to accelerate new masses up to the operating radial velocity before attaching them to the rising chain, and finally thirdly, to release masses in fractional amounts from the top, rather than in unit amounts. The result of these modifications was a fairly smoothly operating siphon simulation model.

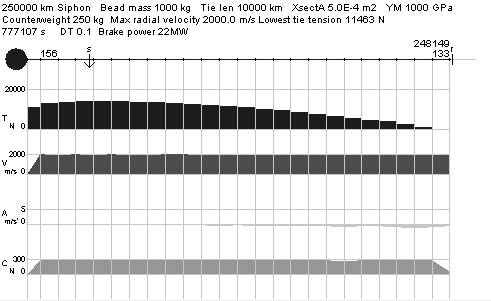
Fig. 7

The simulation displays the rising siphon chain of masses, and the tension, radial velocity, radial acceleration, and transverse coriolis forces. The tension maximum is shown to remain at synchronous, and the radial velocity remains fairly uniform along the length of the chain. The Coriolis forces which act against the rotation of the chain are here calculated by recovering the accelerations discarded to maintain siphon radial motion. Coriolis forces fall at the top of the chain because payload masses are being progressively released in this region.

Engineering Considerations

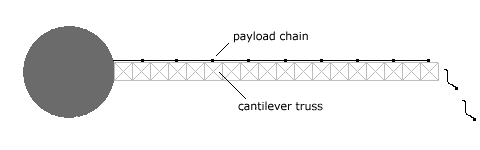
With the simulation model working, the attendant engineering problems needed to be addressed. The first problem was how to lend the siphon sufficient rigidity to overcome the coriolis forces deflecting it as it rose. Since coriolis force is constant along the length of the siphon, at Fc = 2mwv, coriolis forces can be minimized by using small masses rising at low radial velocities. It is probably not necessary for the rising chain to be maintained exactly radial, and it be allowed to bend back from the direction of rotation to some extent. However, some degree of stiffness is required. Several solutions are proposed:

• A cantilever truss along the length of the siphon mass chain, all of whose members would be in tension.
• The mass chain itself to be a rising cantilever truss, with all its members in tension.
• Given that payloads would need thruster motors to navigate once having been released from the siphon, these thrusters, mounted transversely on the the mass chain, might be used to counter coriolis forces.

The engineering problem of braking the siphon appeared best resolved by feeding out the siphon from around the drum of an electric dynamo located at the base of the siphon. The base is anyway the only place where any sort of conventional braking can be employed. The theoretical power input to this dynamo would be the force F exerted by the siphon at its base, multiplied by the radial velocity of the siphon, Vr.

The engineering problem of reducing radial oscillations appeared best resolved by, firstly, using the dynamo brake to slow the acceleration of the rising siphon. Furthermore, the power generated by this brake might be sufficient to accelerate payload masses up to operating radial velocity. And finally, in order to minimize the oscillations due to payload release, payload masses should either be either minimized or incrementally released. This last suggests that a siphon chain should consist of many small masses rather than few large masses.

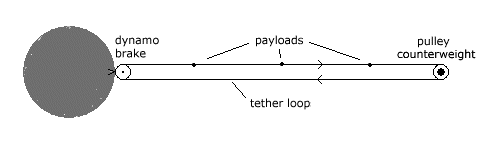
These proposals offer outline engineering solutions to the problems uncovered during the simulation studies. However, there are other problems which the simulation does not address, several of which are concerned with the tether. In the first place, the siphon as described so far would launch long lengths of tether needlessly into space along with the payload masses. One simple solution to this would be to use a tether loop, with one end wrapped round the brake dynamo drum at the base, and the top wrapped around a counerweight wheel or drum at the top. In this manner, only payloads masses would be released from the top of the siphon, and tether would be recycled back round. Such a solution offers the possibility of periodically replacing the tether loop should it become worn or damaged.

Fig. 9

However a further problem with both a single tether and a tether loop is that such tethers must have a uniform croos-section along their length, but the tension maximum in the siphon is at synchronous. Fixed elevator tethers are accordingly tapered for a maximum cross-sectional area at synchronous, to produce a constant stress along the tether. If this is also required for a siphon, then one possible way of 'tapering' a tether loop would be to introduce further tether loops inside the main tether loop, such that they meshed together to increase the cross-sectional area of the tether loop system at synchronous.

Fig. 10

A further possibility would be to mount several tether loops adjacent to each other around the payload mass chain, tied together at their top, so as to distribute stress between them.

An additional problem is posed by the foundations of the siphon, which would be in tension rather than in compression as is the case of terrestrial buildings. The solution would require either the dynamo brake to be secured to the Earth either by a root system extending deep into the Earth, or, more likely, an overmass counterweight to hold down the base.

Given these various proposals for resolving the engineering problems associated with a siphon, they need to be all combined together into a unified whole. And one simple proposal is to mount a tether loop on a cantilever truss. The drum at the base would drive the dynamo brake, and an acceleration chamber below would be used to accelerate payloads before attaching to the rising siphon. The system would be oriented E-W to allow the truss to counter coriolis forces.

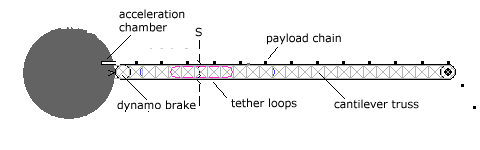
Fig. 11

The construction of such a siphon would begin with a tether loop space elevator, with the dynamo acting as a motor to raise payloads. The entire system would then be extended by increasing the amount of tether ribbon in the tether loops, and constructing the cantilever truss once the required siphon altitude had been reached. The electric motors at the base would then begin raising payloads up the tower until the mass chain began to operate as a siphon, at which point the electric motors would become dynamo brakes.

The initial siphon payload cargo could also be made up of small masses that pulled up heavier ones, until operating payload masses were entrained in the siphon. Equally, in slowing and halting a siphon, the payload masses could be reduced, and the final siphon cargo might consist of small dummy payload masses, used simply to keep the siphon primed for subsequent use. An entire siphon payload train might consist of a head of small dummy masses, followed by a enlarging payload train, followed by a dwindling payload train, and a tail of small dummy masses. Payloads released into space from the siphon would likely not be sprayed in all directions, but retained in a lengthening payload train trailing from top of the siphon, to be daily released all together in some direction.

The principal advantage of an orbital siphon over a space elevator is that whereas a space elevator requires work to be done to raise masses to escape, an orbital siphon leverages energy from the Earth's rotation to raise a continuous stream of payload masses. The only work that is required is to give payloads an initial radial velocity, and the siphon dynamo brakes may well produce sufficient power to do this as well. If payload launch costs for a space elevator are likely to be a small fraction of conventional rocket launches, the launch costs for a siphon are, in principle, zero. However, any siphon would have higher capital costs of construction than a space elevator, and their engineering and operation would be considerably more complex.