Space Elevator Motion

The Effect of Coriolis Forces

While space elevators may mostly be used much like terrestrial airports, with as many spacecraft landing on them and descending as ascend and take off from them, it seems more plausible to suppose that there will generally be a net outflow of mass from a space elevator because some payloads launched into deep space will never return. If space elevators are used to transport materials to construct and maintain very large space stations, it is very unlikely that these materials will ever return to Earth. The only payloads that are likely to return are astronauts - and these will likely form only a tiny fraction of the total payload mass transported up an elevator. So there will generally be an upflow of mass in space elevators.

Given a net mass flow up a space elevator, and that these payload masses climb the elevator at some standard speed, they will exert a Coriolis force, C, against the direction of rotation of the space elevator.

C = 2 . w . m . v

w = angular velocity (radians/s )
m = payload mass (kg)
v = radial velocity of payload ( m/s )

If a more or less constant Coriolis force is going to be exerted against the space elevator, its effect ought to be to gradually slow the counterweight and reduce its altitude, causing the entire elevator to swing back against its rotational path of motion.

It seems perfectly plausible to suppose that the end result of a continuous exertion of coriolis forces against the direction of elevator motion will likely be the collapse of the elevator.

An Elevator Simulation Model

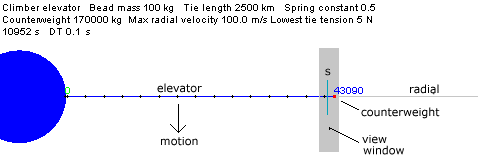
One way of studying this circumstance is to build a simulation model, and see what happens. The Elevator.java model is a variant of the siphon simulation model. A counterweight is placed just outside geosynchronous orbit, and connected to the equator by a cable consisting of a number of point masses connected by massless cables. This tower is then subjected to coriolis forces. Three different ways are used to do this. In the first, a static tower has Coriolis forces exerted on all the point masses in the tower below synchronous. In the second model, the counterweight has a lift engine that hauls up the chain of masses below, releasing them when they reach the top. And in the third simulation, the chain of masses climbs the cable to the counterweight, and each mass releases itself into free orbit when it reaches the counterweight. The tether is not tapered. The motions of masses are calculated using only Newton's laws of motion and gravitation, and Hooke's law of elasticity. The forces exerted upon any body in the tower are calculated, and from that their acceleration, and from that their motion over a short time interval is calculated. The time interval is a matter of some interest, and in the the critical cases this interval is varied to maintain movement over around 50 metres.

Of the three simulations, the lift engine simulation is arguably the worst simulation, because as the lift engine hauls up the chain of masses, it regularly jerks new masses up from the planet surface, generating strong radial oscillations (much like in the siphon simulation). The Coriolis force model, by contrast, has very little radial oscillation, but nothing is actually moving up it, or being released from it. The climber simulation model, by contrast, actually has masses moving up it, and being released from it, and is subject to far less radial oscillation than the lift engine model - largely because new masses are given an initial radial velocity. And so the results here are largely taken from the climber simulation.

Simulation Model Results

The simulation model was used to examine the behaviour of an elevator counterweight, firstly without any climbers, and then with payloads climbing the tether. The counterweight was positioned at a radius of 43,000 km, just outside synchronous orbit radius of 42,172 km, to deliberately ensure that the elevator would be near its limit of stability. And then the counterweight mass was reduced so that the elevator was at its limit of stability.

The study centred on following the motion of the counterweight, using a view window that centred upon it and its immediate environs.

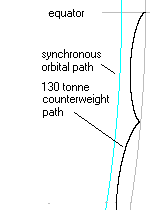In general, with counterweights on the static towers greater than about 130 tonnes, the elevator tower remained stationary. 130 tonne or less counterweights were insufficient to maintain the tower upright (see right), and it fell forwards and downwards along the direction of motion of the elevator tower, eventually wrapping itself almost entirely around the surface of the Earth.

In the second case, the same set of towers had the masses below the counterweight climb the tether at a constant speed. Counterweight motions are now markedly different. In the range of elevators from 140 - 210 tonnes, the counterweight loses altitude, and falls forward along the direction of motion of the elevator. Only counterweights above 230 tonnes remain in place, and swing E-W, but with the swing displaced away from the direction of motion. A 220 tonne counterweight remains in place for 8 million seconds, but its uneven oscillation suggests that eventually it may also fall.

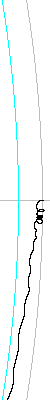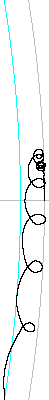140 T	170 T	190 T	200 T	210 T	220 T  8 M s	230 T  1 M s	300 T  8 M s
Counterweight motion trails in an elevator with rising payloads. The gray arc is the stable counterweight radial path, and the blue arc is the synchronous path. T is tonnes counterweight mass. The direction of elevator motion is downward, and Earth is to the left (S pole view).

The effect of coriolis forces should be to move the counterweight downwards and backwards. In the 140 and 150 tonne cases, it appears to act entirely downwards. But with higher counterweight masses, it appears to act to reverse the counterweight backwards, and to cause the counterweight to revolve in a circle as it moves. This circling motion largely ceases with counterweight masses above 220 tonnes, which maintain a largely even swing.

Also notable is that the swing amplitude of larger counterweights decreased with mass. And that the maximum swing amplitude of the 210 tonne model did not complete the swing amplitude suggested by greater masses.

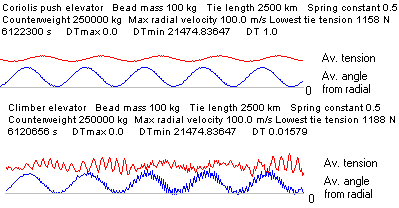
Comparisons of the Coriolis-push and climber simulations show very similar swing periods and amplitudes. The climber simulation is noisier because, in part, there are events such as payload releases taking place.

One slightly surprising discovery was that the tether "twanged" like a guitar string.

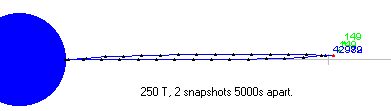
The effect of this must be that tether tension oscillates in frequency with the twang, and this affects the motion of the counterweight - perhaps generating the circling motion noted earlier. The 'twanging' effect wasn't found with the coriolis-force-pushed static tower simulation model, but only in the climber simulation model. Plots of of average angle from radial, and average tie tension, show strong oscillations in the climber model.

Also it was found that if climbers stopped on an elevator, and coriolis forces ceased to be exerted against the elevator, it continued swinging, but this time around the radial axis.

Conclusions

The principal aim of the study was to see how space elevators behaved with rising streams of masses. Other studies have suggested that space elevators swing back and forth. My suspicion was that coriolis forces might cause elevators to collapse. Both the earlier studies and my suspicions seem to have been confirmed.

It appears from these simulation results that coriolis forces can indeed bring down space elevators, but only those with low counterweight masses. Higher mass counterweights first swing back from radial against their path of motion, and then swing forward towards radial, and keep on swinging backward and forward more or less regularly, generally trailing behind radial.

This is a very simple numerical simulation model. The elevators examined here are unlike proposed elevators, in that they are not in constant tension along their length. And a relatively small number of masses is used to simulate both tether and rising masses. One disadvantage of such models is that, depending on the power of the computer used, they need to be run for long periods. The results show that elevators with relatively low mass counterweights do indeed collapse, but the results may not be showing that elevators with higher mass counterweights stay up indefinitely. That could only be found out by running the simulation indefinitely. As it is, the longest period of time they have been run is some 100 days of real time, which isn't very long. It might be argued that coriolis forces cause low mass elevators to collapse more quickly than high mass elevators, and that every elevator has a lifetime.

However, all the elevators that failed did so rapidly, before completing a single swing, and all the elevators that stayed up kept on swinging. There were no examples of elevators that performed several swings and then failed. So it would appear that there is neither a 'lifetime' for elevators, nor that the simulation simply didn't run long enough to reach the expiry of this lifetime. Instead it appears that elevators either rapidly collapse, or stay up indefinitely.

The best conjecture seems to be that swinging elevators get a regular tug or pull from the rotating Earth on their backswing, and this is sufficient for them to stay up indefinitely. Elevators that fail are ones that just never got that extra tug in time to prevent coriolis forces pulling them down.

[ Postscript: despite efforts to reduce radial vibrations, this simulation model is still fairly 'noisy', and it may well simply be radial oscillations which bring down the lightest counterweights.]

Possible further studies

The conclusions drawn from this study are only of a tentative, preliminary character. The simulation model could be altered and improved in many ways. This suggests further studies.

This suggests a further study to see whether elevators are being given a regular tug from the rotating earth. In the present study, the Earth is simply given a fixed period of rotation equal to one sidereal day. An extended study might model the Earth, or an asteroid, as a set (perhaps a circle) of connected masses revolving round a central point. These masses would be subjected to similar forces as those in the elevator. If the planet mass was set low, and the elevator mass high, then if the planet was giving the elevator a regular tug, the result should be a perceptible slowing of the rate of rotation of the planet.

Another approach might be to consider the elevator as a store of energy, able to perform some amount of work in raising mass from the surface of the Earth. In failing elevators, it might be supposed that this store of energy is rapidly dissipated. In successful elevators, it might be shown that the energy is partly dissipated and then recovered.

Improvements to the model might include: 1) using more bodies to simulate the tether, 2) allowing for varying tether crossectional area, 3) using standard Young's modulus values, 4) separating payloads from tether, 5) accelerating climbers slowly up to maximum speed, and deccelerating to halt when they reach the payload.

Another study might be of payload paths. The present model simply releases payloads just before they reach the counterweight. Because the tether is swinging, this can result in the payloads flying off in all directions.

It may also be possible to numerically simulate thruster motors on payloads, by spraying out part of their mass in some direction and at some velocity. This might then be used on the siphon model to provide lateral thrust to counter coriolis forces, and maintain the siphon radial or near-radial. It might also be used to simulate conventional rocket launches. And, since it can be argued that all payloads should carry thruster motors, both for navigation after release from elevator or siphon, and in the event of elevator or siphon failure, failure mode studies could include the use of thrusters to avert disastrous Earth impacts.