The TETRA model

In the second model, the TETRA model, the principal conclusion of the MALTHUS simulations - the survival of the idlest - is adopted as a premise, and a different approach is taken to simulating population expansion and Malthusian crisis. In this model, I attempt to construct animals which obey the laws of physics, at least in a simplified form. In the TETRA model, S.I. units of mass, length, and time - kilograms, metres, and seconds - are employed. The grazers of the TETRA model are feeding engines of specific sizes with calculable characteristics. When the TETRA model evolves a new animal, it tries to estimate what the performance characteristics of the animal would be, given what is known about it, rather than simply asserting those characteristics as arbitrary fiat. Thus, given the size of an animal, its weight and surface area can be deduced. And if its metabolic rate is a function of its surface area, then its metabolic rate can also be deduced, and so on. Again, the animals of the TETRA model are simplifications, wind-up toy animals, and the greater bulk of their metabolic processes are either omitted or generalised.

The TETRA model, furthermore, deals with aggregated populations and averaged 'grass' density. While MALTHUS has individual clumps of grass being sought by individual grazers, the TETRA model has entire perfectly-dispersed populations grazing on an undifferentiated field which is no thicker in one place than in another, and are treated on a population per square metre basis. And while the MALTHUS model, populations drop out from the reproductive characteristics of the individual grazers, in the TETRA model populations are estimated from overall birthrates and deathrates. Equally, while there are strong random elements in MALTHUS, the tetra model is entirely non-random. Thus if the MALTHUS model employs simple addition and subtraction to randomised, probablistic, discrete particles, the TETRA model employs some relatively complex mathematics to a non-random, averaged field. Essentially, however, they are both modelling the same thing.

Ideally, the two models should be combined. Either the MALTHUS grazers should be constructed to obey the laws of physics, or the results of the MALTHUS simulations should form the basis of the generalised TETRA calculations.

The purpose of the TETRA model is to see what happens when a physically-plausible model animal is allowed to multiply and diversify indefinitely.

Theory:

The metabolism of a living organism - plant or animal - requires a supply of energy. In this respect, it is no different from an automobile engine, or a television. Automobiles burn energy in the form of gasoline. Television sets consume energy in the form of electricity. Plants are powered by the energy of solar radiation. Animals run on the energy content of the plants or organisms they eat.

A living organism differs from a simple machine in that it not only uses energy, but it must also expend energy to replace what it uses. the simplest circumstance, an animal busies itself replacing energy, and then idles until it needs to acquire more. In any period of time, therefore, some of the time is spent idling at a reduced metabolic rate, and the remainder is occupied with more energetic work.

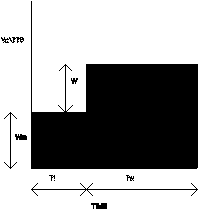
In Figure 10, the example shows an animal which is working for about 60% of its time, and is idle for the remaining 40%. During its idle time, Ti, it uses energy at the rate Wm watts, and during its working time, Tw, it uses energy at an extra rate W. The actual range of possibilities are that an animal could be idle for anything between 0% of its time - when it would be working all the time -, and idle for nearly 100% of its time - when it would it would be doing next to no work -. And there is also the possibility that an animal may have to work more hours than there are in a day to replace the energy it uses in a day. This is clearly an impossibility: such an animal cannot survive. It would die. The animal that works all day to replace the energy it uses in a day is a borderline case. So if an animal is to survive at all, it must be idle for some part of its time.

If Tw is the working time/ day - where a 'day' is simply some unit period of time -, and Ti is the idle time/ day, then

	Ti + Tw = 1						(1)

and the Idleness, I, which is the fraction of the day that is spent idle, is defined as

	I = Ti / ( Ti + Tw )				(2)

with 1 >= I >= 0 defining a living creature, and I < 0 a dead one.

Work, for a grazing animal, roughly involves expending energy moving towards, chewing, and swallowing food, the calorific value of which gives the energy acquired. If the ratio of the two is called K, then

K = energy acquired / energy expended

such that if the creature works at a rate W joules/sec for a period of time T_w, the amount of energy it acquires, Q_in, is given by

	Qin = W.K.Tw joules							

Idling, for a grazing animal, involves an energy expenditure, Wm joules/sec, which corresponds to its basal ( resting ) metabolic rate. If throughout the day the animal expends energy at the rate Wm, and during work periods it expends additional energy at the rate W, its daily expenditure of energy, Q_out, is given by

	Qout = Wm + W.Tw joules

At balance, where the animal acquires what it expends,

	Qin  = Qout

so	W.K.Tw = Wm + W.Tw

and	Tw   =  Wm / ( W.( K - 1 ) )			(3)

and from (1), Idleness , I, is:

     
           I =  1 - Tw									
             =  1 - ( Wm / ( W.( K - 1 ) ) )		(4)

and where W(K - 1) is greater than zero, 0 < I < 1.

The equation confirms what one may have suspected: the lower the basal metabolic rate, Wm, and the higher the amount of energy an animal acquires per unit expended, K, the more Idleness, I, increases.

Figure 11 The model animal is a simple cube-shaped 'tetrapod' - intended to represent a grazing animal -, with 4 legs, and a mouth which it uses to chew through an energy-rich theoretical pasture rather like a lawn-mower through grass. This tetra will have a simple, even tedious, life of either 'working' by walking slowly forward eating, or 'idling' by standing still.

The theoretical pasture is intended to represent a flat grassland that has a constant depth, density and calorific content ( which I will refer to as 'energy density', J/m³ ).

For its basal metabolic rate, Wm, I will adopt that of a human adult - about 30 watts/square metre of surface area. (This is Rubner's Surface Rule, and is rather inaccurate, but suffices for the purposes of this simple model.) And for the rate at which the tetra can work above basal,W , I will assume a modest multiple of 3. Human beings can actually manage considerably more than this, so it's a conservative figure.

As the tetra moves forward, it does work at a rate W in moving its body mass forward, in shearing through the pasture, and in raising the food up to its digestive system. Given that the tetra performs a calculable amount of work for each metre it moves forward, and in doing so ingests a volume of pasture with a known energy content, the value of K can be found. If a tetra leg swings like a pendulum, the speed at which it walks forward can also be found.

In performing physical work - walking, chewing, swallowing - the tetra is also assumed to be only 25% efficient: i.e. only a quarter of the energy it expends actually translates into physical work. This again is the same as a human being. The tetra is also assumed to have a density similar to that of a mammal - roughly the same as water -, and to have square bones in its square legs which have the same physical characteristics as bone.

The tetra's internal metabolism is, by contrast, a 'black box'. It is simply assumed that all the energy in the food swallowed by it is absorbed and stored, and that it can 'digest' food at whatever rate it consumed it. The tetra's internal energy transport system is not modelled, and is assumed to be able to deliver energy at whatever rate is required, within the constraint that the overall energy usage does not exceed a fixed multiple of basal metabolic rate. Neither is the tetra's musculature modelled, but is assumed to be able to perform the work required of it.

Given the body size, and head and leg proportions, the volume, Va, mass, Ma, and surface area, Aa, are readily calculable.

The leg thickness of the tetras increases in proportion to the mass of the tetra itself, which means since mass increases with the cube of volume, larger tetras require proportionately thicker legs. Equally, and perhaps rather pedantically, the very thin legs of the smallest tetras are thickened, using Euler's Column Formula for pin-ended columns, to avoid lateral buckling.

The basal metabolic rate, Wm, is assumed to be proportional to surface area. Assuming a constant heat loss of Wpa W/m² , and using the surface area equation (10)

	Wm = Aa.Wpa						

The energy that the tetra performs while feeding breaks down into

• the work it does in moving forward bodily,
• the work it does in cutting through the pasture,
• the work it does in raising food up to the top of its digestive tract.

In moving bodily forward, the tetra takes strides such that at full stride the body mass is lower than when the animal is standing with both legs vertical. Thus each step involves lowering the body mass ( at no cost ), and then raising it back up. If H is the height the body must be lifted with each stride, the energy expenditure/stride is

	Ma.g.H

This is equivalent to rolling a polygon along its sides, with each side representing a stride. The kinetic energy component, required to get the tetra moving forward, and stopping it again, is ignored.

If the angle between the 2 legs is defined as 2.T, and the leg length is AS, then

	H = AS(1 - COS(T))

and energy expenditure/stride, Q₁, is given by

	Q1 = Ma.g.AS(1- COS(T))					

The energy expenditure / stride in cutting through the pasture is taken to be a constant ( regardless of the size of the animal ) per unit volume of pasture, so that

Q2 = F-shear x volume cut through / stride.

	   = F-shear x stride length x mouth width x mouth size

	   = F-shear . 2.AS.SIN(theta) . S	. CA				

The energy expenditure/stride of lifting the cut pasture, Q₃, is given by

Q₃ = mass of food x g x height lifted,h = stride length x mouth width x mouth height x g x h = 2.AS.SIN(theta) . S . CA . g . AS

The animal moves by swinging its legs at a rate which corresponds to the natural period of a compound pendulum, whose length is less than the fully extended length of the leg. The period of a compound pendulum is

2.pi.( 2.l / 3.g )^.5

and with a stride taking one half period of the leg swing,

stride time = pi.( 2.AS.COS(theta) / 3.g )^.5 and forward speed = stride length / stride time

As the work done/stride is the sum of Q₁ + Q₂ + Q₃, the rate at which work is done, W, is given by

W = (Q₁ + Q₂ + Q₃) / stride time

As the stride angle increases, therefore, the animal does more work lifting its body with each step, increasing Q₁, and also does more work as it cuts through and lifts a larger amount of pasture, in the same unit half period, so W increases.

A further restriction is placed upon the stride angle, such that the work rate, W, does not exceed the ability of the organism to mobilise internal energy resources.

With maximum work rate, W, set as 3 times basal metabolic rate, pasture energy densities constant with depth, the largest animals tend to have energy requirements in excess of 3x basal metabolic rate, and therefore have stride length curtailed to restrict them, with a consequent fall-off in efficiency. The smallest animals tend to be underusing their power capabilities. Figure 13 - constant proportions

With Idleness plotted against increasing body size , expressed as powers 10ⁿ metres, and each curve representing a doubling of energy density in the pasture, with 1x10⁵ J/m³ as the minimum value, the set of curves in Figure 14 is obtained.

This is an interesting set of curves. As energy densities increase, idleness increases, and a larger range of animals become viable. The sharp cut-off at about 10^2.3 metres arises where animals have become too heavy for their legs to support.

With the selected data, this shows that much below 10⁵ J/m³ none of these animals are viable, and that at 16.10⁵ J/m³ a quite large range of them are nearly 100% idle, and it is surprising that the switch from non-viability to near-complete idleness should take place over such a narrow range. It suggests that, in all possible universes, the chances are that viable animals will be for the most part nearly completely idle.

One clear observation is that, in the range of viability, Idleness optimizes at a middle range. The reason that the very biggest tetras aren't optimal is because the restriction of W = 3.Wm tends to come increasingly into play after about 10^-2 metres. Larger viable tetras are increasingly constrained by their limited energy budgets to shuffle along with short steps, while smaller tetras find that they have more energy available than they can effectively use, and are conversely inefficient. Above 10^2.4 metres, the leg size required to support the animal tends to become infinite, as the animal is virtually all legs, and this gives the maximum size of animal possible.

Another clear observation is that as energy densities increase, the 'island' of viability widens, with both larger and smaller tetras becoming viable.

Another interesting feature of these 'islands' of viability is that they tend to be steep-sided peaks, rather than low flat hills. As energy densities increase, the result is not a progressive widening with a slightly higher peak, but a slight widening with a progressively higher peak, which rapidly approaches its limit of 1.0. At the higher energy densities shown in Fig.3, the islands of viability have plateau peaks just below I = 1.0, and rapid fall-off at the extremes. If animal population numbers are taken to be constant at all scales, then most animals would be very idle, with only a few at the very largest and smallest showing much sign of activity.

The islands also provide an interesting commentary on the MALTHUS models. In MALTHUS, a characteristic such as lower consumption, higher speed, or larger energy store, tended to have no optimum: the more the merrier, as it were. A similar set of graphs for MALTHUS would have shown no optima, and no islands of viability.

The set of curves in figure 14 represents the range of viability of one particular tetra, which has the same proportional mouth height and leg length whatever size the body is. If however, the legs and mouths are optimized at each size, to give the maximum idleness, a slightly different picture appears. In figure 15, the set of curves shows the islands of viability when the tetras have been optimized. Figure 14 - optimised leg and mouth proportions

In this case the islands of viability have widened, and show distinct plateau characteristics. In the plateau region, there is for the most part no clear optimum leg or mouth size. In small scale non-plateau region, however, the tetras optimise with long legs and large mouths. In the large-scale non-plateau region, the tetras optimise with very short legs, and large mouths. Thus the left-hand end of the island - the 'west' coast - will be populated by small, long-legged tetras, while the 'east' end of the island will be occupied by large, short-legged ones, with a wide variety in the middle. This seems to very roughly conform to real life, where small insects appear general to have proportionally longer legs than larger organisms, and where the largest animals - crocodiles, rhinos, hippos - often have relatively short legs. In regularly opting for the biggest possible mouth, the TETRA models indicate that there is no optimum within the given constraints.

I have no explanation of the plateau character of these optimisations. It is not immediately obvious that the mathematics should produce such a result. In a more complex model, they might well vanish.

In the model constructed so far, tetras are either viable or non-viable, and those that live are implicitly assumed to live indefinitely. In reality, living organisms have limited lifetimes. There are several ways in which tetras could die:

1. They might have a fixed-duration 'natural' lifetime.
   
2. They might be subjected to corrosion death, 'rusting' into immobility.
   
3. They might undergo death through wear or fatigue, where minute fractures compound into general failure.
   
4. The existence of islands of viability suggest that if tetras have small size at birth, and grow steadily throughout their life, this growth might 'walk' it from one end of the island of viability to the other. New-born tetras would be nearly non-viable, but would rapidly increase in efficiency, until they got 'over the hill', after which they would become steadily less efficient, and less idle, until on the far shore they would succumb as idleness reached zero.

This last is a rather compelling possibility, but unfortunately I have no proposals for tetra growth. In the simplified tetra reproduction scheme (to be discussed shortly), tetras appear full-sized from the outset, and do not grow at all, so this option cannot be adopted. A 'natural' fixed lifespan has its attractions, but there is no obvious way of saying what is 'natural' for any tetra. The corrosion death model would require additional elements to the model. Thus for the purposes of this simulation, I will employ a simple fatigue-death model.

Metal fatigue in machine parts is the result of repeated loading and unloading of a component, and the magnitude of the stress required to produce failure decreases as the number of stress cycles increases. Fatigue results in the formation of minute cracks which progressively enlarge to the point of catastrophic failure. The legs of the tetras, while adequately sized to support the load, are subject - as they walk forward - to exactly the cyclic loading and unloading that results in fatigue failure. Thus it seems reasonable to suggest that, since the leg stresses in all the animals are of the same order regardless of size, fatigue failure, and death through immobilisation, will occur after a some number of steps.

There is some empirical evidence that, among mammals at least, the number of heartbeats in the life of a mouse and an elephant are approximately equal.

The number of steps a tetra takes in a lifetime is equal to the duration of its working lifetime divided by the swing period of its legs:

lifetime-steps = lifetime.(1 - Idleness) / leg-period

so

lifetime = lifetime-steps.leg-period / ( 1 - Idleness ) and deathrate = 1 / lifetime

Since larger tetras have longer legs, and longer leg swing periods, larger animals will tend to have longer lives, which seems to accord with real life, where the largest animals have the longest lives. Also, as idleness increases, lifetimes get longer. Using this approach, interestingly, if idleness ever reaches 100%, the tetra is immortal.

With death introduced into the picture, a compensatory birthrate is required if the tetras are not to simply die out. Furthermore, tetras with the highest death-rates must have correspondingly high birth-rates.

Much as with death-rates, it isn't immediately obvious what defines birth-rates in a tetra or any real animal. Reproduction, however, must entail the expenditure of energy in synthesizing proteins to construct a new tetra. At very least, some of a tetras energy has to be diverted in this direction. One simple approach is to assume that reproduction is a constantly continuing process. In reproducing, a tetra might be assumed to steadily construct a full-size replica of itself, and it seems reasonable to suppose that some proportion of its basal metabolism is continuously involved in this reproductive work, just as much as it is involved in breathing or pumping blood, and that when it has finished making one, it starts on another.

Assuming that there is an energy cost, Cr, per m³ of body constructed, and that a fraction, repro, of basal metabolic rate is expended in continuous production, then the period of time it takes to produce a complete replica is

body-volume.Cr / repro

and birthrate = repro / ( body-volume.Cr)

Since the smallest tetras have the highest metabolic rates, their birth-rates will be correspondingly higher, and this should be able to compensate for their high death-rates. The rate at which the population is growing is thus given by:

growth-rate = ( birthrate - deathrate ). population

and over a period of time the population is given by

population = initial-population.(1 + growth-rate)^period

which is growth at compounding rates.

Figure 15

Assuming 10⁸ steps in a lifetime, and an energy cost/m3 of reproduction equal to the consumption calorific value of some kind of meat, at 1.67.10¹⁰ J/m³, and 1/6th of basal metabolic rate devoted to reproduction, Figure 16 shows birthrate - deathrate for the range of tetras and energy densities already displayed. These show net growth rates increasing by a factor of 10 for every factor of 10 decrease in tetra size, indicating that there isn't going to be a problem of deathrates exceeding birthrates. It is not shown, but some of the largest tetras have negative growth rates where idleness is low. Reproduction is asexual, and each type of tetra produces an exact replica of itself.

If evolution is going to occur, however, tetra reproduction should occasionally result in a mutant tetra. The TETRA model assumes a 'single gene', which determines tetra size. A small fraction, Fmutant, of tetra births are mutants, one size larger or smaller. Mutant tetras are either 3 times larger, or 3 times smaller. This is a fairly substantial increment, adopted to minimise the number of populations of each size of tetra, and maximise the range of possible tetra sizes. The upper size limit is defined by maximum leg size, and the smallest is arbitrarily chosen to be 10^-6 metres side length. There are no 'saltations': the tetras can only diversify step by step in two directions: bigger or smaller. A naming convention, tetra-x, is adopted, where '-x' gives the tetra side length according to the formula 10^-x. Thus a tetra-6 is a tetra with a side length of 10^-6 metres, or one micron. In any period of time, the mutant population produced by a single tetra type will be given by:

mutant-population = population.birth-rate.period.Fmutant

Thus high populations, and high birth-rates, over long periods, will produce the most mutants. Fmutant, in this model, is of the order of 10^-8, or 1 in 100,000,000. For a mutant population to become established, the mutant population must be >= 1, and the mutant must be viable - i.e. I > 0 -. A population of one variety of tetra may thus be producing numbers of non-viable offspring, whose fate is to promptly die. Adjoining populations may also be feeding each other's populations.

With tetra characteristics calculated, the model is initialised with a small population of tetra grazers which proceed to multiply precisely along the lines of the MALTHUS model. Tetra energy uptake from the pasture is the sum of the entire population's consumption. The pasture itself has a constant energy intake which is a photosynthetic fraction of the Solar Constant. If pasture intake exceeds uptake, the pasture energy density rises. In the converse case it falls. As pasture energy density changes, tetra K values - the amount of energy received for unit energy expenditure in grazing - is recalculated, and idleness re-evaluated. As pasture energy density falls, the tetra grazers have to work longer. As it rises, they work less.

Figure 17 shows the result of exact reproduction (no mutants) of a standard tetra, combined with fatigue death. The pasture is assumed to increase its energy density linearly with time, as it photosynthesizes solar radiation. The pasture, at the same time, is having its energy density reduced by the tetras which feed off it. At time 0, the population/m² of tetras is very low, and energy densities gradually rise as the pasture 'grows'. Tetra idleness is almost constant over the initial period. As the population multiplies it begins to extract energy from the pasture at a greater rate than it is being replaced, with the result that the mean energy density of the pasture begins to fall, and with an increasingly energy-poor pasture the tetras have to work harder. As the population continues to grow exponentially, the pasture energy density drops faster and faster, and tetra idleness decreases. Finally, when tetra idleness reaches zero, the entire population - which is still increasing - abruptly dies, and the tetras become extinct. Energy densities have fallen to less than 1/4th of their original values, and thereafter gradually recover.

Figure 16

This simple run immediately demonstrates a difference from MALTHUS. In the equivalent MALTHUS run (Figure 6), the multiplying population crashes, but does not always become extinct. In fact, the usual result is for the population to collapse to a low level, and then make periodic recoveries. Also idleness in the MALTHUS model tends to follow an irregular pattern. The TETRA model, by contrast, produces nice smooth curves and total extinction.

Figure 17

When the tetra population begins to reproduce inexactly, a different picture emerges. The rising populations generate the usual overgrazing problem, and falling pasture energy densities bring increasing work rates for all grazers, and only the idlest survive the subsequent extinctions.

Figure 17 shows the family tree of different sizes of tetra over time. The tree also shows log population on each limb, with each step representing a 10-fold increase in population. A graph above shows pasture energy density as time passes. Initially, a seed tetra with a body size of 10^-6 metres - a tetra-6 - with a population density of a single individual begins reproducing itself. After a while, with 1 in 100,000,000 births being one size bigger or smaller, a tetra-5.5 appears, and then a tetra-5, and so on until a tetra-1.5 ( about the size of a matchbox ) completes the range.

However, as larger tetras evolve from the first tetra-6, the total population rapidly starts to overgraze the pasture, and a series of Malthusian crises develop, which result in the extinction of the smallest and least idle tetras. The small tetras rapidly re-evolve after each extinction. The crises, however, get deeper and deeper, until at one stage only a small population of tetra-2.5s and tetra-2s remains, and a relatively slow re-diversification towards the smaller scale follows, during which the pasture energy density - the 'lushness' of the vegetation - climbs off-scale. After a further series of extinctions and rediversifications, the final grand extinction claims the entire range of tetras.

In figure 14, the smallest island of viability includes the tetra-2s and tetra-2.5s: they are the only ones that can live at such low energy densities, and are the last to die out. In Figure 17, the populations of tetra-2.5s and tetra-2s gradually rises until they are the principal grazers, and are holding down pasture energy density with their own numbers alone. In the final Malthusian crisis, after 42 million seconds, first tetra-2s, and then tetra-2.5s drive down pasture energy densities to the point where they too become extinct.

The evolution of tetras also proceeds more rapidly towards the smaller end than the larger. The reason is that the smaller tetras, with their high reproduction rates, generate large populations rapidly, and consequently produce mutants more rapidly, and do so faster and faster the smaller they are. By contrast the slow-growing populations of larger tetras produce larger mutants more slowly, and it takes longer and longer for successive large-scale tetras to appear. Some never do.

The initial populations of tetras, particularly in the re-diversifications, may appear to be unexpectedly high: a lot of them appear at once. But then, in the intervals after extinctions and before re-appearance, there is a constant stream of non-viable tetras being produced at the edge, and promptly dying. Every tetra population, once it has expanded to the point where it is generating mutants, has a 'bow wave' on either side which is either added into an existing adjacent population, or vanishes in instant extinction. This 'hidden' population may be quite high, so that when the variant become viable, a lot appear at once, and the population expands from a large base, and which continues to be fed by the adjacent population, artificially enhancing its natural growth rate.

The overall process is one of pasture over-grazing, followed by extinctions, and then pasture recoveries. This agrees broadly with the MALTHUS model. However the TETRA model, dealing as it does with aggregated populations, produces aggregated extinctions - they either all live or they all die -, and it is questionable whether it would actually be quite like that. However, since during the major extinctions the pasture energy density is falling, and continues to fall as the individual species of tetra drop out, a MALTHUS model would probably also produce an extinction in most of these cases. There are two exceptions to this, though. The first is where a tetra extinction marks the end of the crisis, and the beginning of pasture recovery, as is the case with the first extinction of tetra-3s. Here a MALTHUS model might show a fall in numbers, but a small continuing population. The TETRA model compensates, perhaps, by rapidly re-evolving tetra-3s in this case. The second exception is in the final extinction. A MALTHUS model would most likely show the population of tetra-2.5s and tetra-2s collapsing, but not necessarily becoming extinct. The pasture would recover, and tetra populations would expand from a small base of tetra-2.5s and tetra-2s to generate a series of new crises. Nevertheless, there is a chance that one of the final crises would bring the tetra era to an end.

More generally, Figure 17 is interesting in that new types of tetra do not appear at regular intervals. 'Evolution' appears to be run rapidly at the outset, producing many variants in a short time, and then to slow up and be then punctuated by sudden re-radiations. While the usual picture of the evolutionary process is one of slow and gradual change, the overall picture that emerges here is one of long term slow change interrupted by 'sudden' change. The initial diversification is sudden. The extinctions are sudden. The re-diversifications are sudden.

Another interesting feature of Figure 17 is the population peaks. The micron-sized tetra-6s achieve population densities of nearly 10¹² / m², which has them completely carpeting the pasture in a seething mass. The sugar-cube sized tetra-2, however, only achieves maximum population densities of about 1 per square kilometre.

The main problem with the grazer population is that they are doomed to extinction. In detail, the span of the tetra era is determined by the time it takes for the idlest tetra to multiply to the point where its own population is the principal cause of a collapse in the pasture energy density, and its own extinction. The idlest tetra is tetra-2.5, and the tetra era ends (in the TETRA model at least) when it brings extinction upon itself, and by inference on every other less idle tetra. Since there are no idler tetras, tetra-2.5 is the last to go.

The TETRA model, thus far, consists entirely of grazers on a grassland pasture: i.e. of 2 trophic levels. There is absolutely nothing to stop the tetras multiplying except the regular arrival of Malthusian crises. If the tetra 'era' is to be extended, some way has to be found to restrict their numbers.

One possible solution to this problem is to introduce predators. Before one can introduce predators, however, some sort of explanation has to be given for their arrival on the scene. Predators are unlikely to appear, ex nihilo, fully equipped with razor-sharp teeth and claws. Predators, like everything else, have to evolve.

The explanation I offer for predation grows directly from the primacy of idleness in the "survival of the idlest". The tetra grazers so far discussed have only one means of subsistence: feeding on the grasslands. And their lives are easier or harder as the grass is thicker or thinner. But the grazers periodically die, either of old age or at the nadir of a Malthusian crisis. Thus the grasslands will be strewn with the remains of dead grazers, which some grazers will encounter from time to time, and which some are quite likely to consume, simply because they constitute a rich food source. In a developing Malthusian crisis, where grass is thin on the ground, and grazers are dying in droves, such an omnivorous scavenger would very likely find that the Malthusian crisis generated a bounty of food, and would perhaps find itself surviving the crisis. After the crisis was over, and the grass began to thicken, and the decimated grazer populations left few bodies, such an omnivorous scavenger would revert to grazing. Having survived the crisis, it would then multiply through the upwave as the grass thickened, and continue to eat its mixed diet. And if dead grazers provided a richer source of energy than grass, such scavengers would lead an idler life than their grazer cousins. The step from scavenging to outright predation is short: the predator doesn't wait for the grazers to die, but actively assists the process. At the outset of predator existence, grazers might not try to escape, and predation might not be significantly more difficult than scavenging. But if some grazers did flee, as time went by the predators would tend to select out the non-escapers, and generate a population of fleeing grazers. Predation would then increasingly involve pursuit and capture.

The essence of the argument here is that, where an omnivore has a choice, it does the easiest thing. If grass grows thickly and abundantly, it opts for grazing. If grass is thin, and dead grazers abundant, it opts for scavenging. If grass is thin, and dead grazers are not abundant (perhaps because of the activities of other scavengers), it opts for predation. In this view, the grazer-scavenger-predator is not locked 'by nature' into being either a grazer or a scavenger or a predator, but is akin to a diligent share portfolio manager, always looking for the best return, selling shares in grass as the pasture thins and buying into the meat market, and vice versa when the market changes.

That said, it is quite likely that such versatile omnivores could get 'locked in' one mode of existence. In a long period of rich grass, some might tend to specialise as grazers, and lose the ability to hunt. Equally, in a long period where game is abundant, an otherwise versatile omnivore might become a full time predator, and lose the ability to graze.

In the TETRA model, the predators are all versatile omnivores who can eat anything. In fact, the entire range of tetras is assumed to be omnivorous. And it is assumed that predation involves the pursuit and capture of one fleeing tetra by another.

In the predator versions of the TETRA model, the tetras make choices. The grazing option involves an expenditure of energy moving and eating, and a return which is defined by the energy density of the grass. i.e. there is some K value associated with grazing. The various predation options present themselves in essentially the same form: some amount of energy must be expended in pursuit and capture of another tetra, and success yields a return in the form of the energy content of the captive. i.e. there is a K value associated with each potential target. The amount of energy expended in pursuing a target tetra depends how far away the target is from the predator, and how fast it runs. The amount of energy the predator receives after a successful pursuit is determined by the size of the captured tetra.

In the TETRA model, the mean distance-to-target is taken to be the mean distance between the individuals in the target population. Thus if a target population has a density of one individual per square metre, the mean distance between them is taken to be one metre. Tetra predators use this information, combined with their own top speed and the target tetra's top speed, to calculate their energy expenditure of pursuit (capture assumed to have no cost) and the resultant K value of success. The result of a survey of all possible targets, including the grazing option, produces a menu of K values. The predator-grazer selects the highest K (which maximises idleness) option, whatever it happens to be.

Figure 18

Predation along these lines relies on some grazers being faster than others. Figure 18 shows the forward speeds of the tetra range while grazing or running. The difference between the two arises because a grazing tetra is not only moving forward, but also chewing and swallowing, and its energy budget has to be divided between these. When running, all available energy is devoted to forward motion. The result is that the smallest tetras, which have such high metabolic rates that their legs can't move them fast enough, show little or no speed improvements. The larger tetras, whose lower metabolic rates restrict stride length, are able to convert the extra available energy into significant speed increases. Thus while the fastest grazing tetra is tetra-2.5, the fastest runner is tetra-1. Thus tetra-1 is potentially the top predator, because it can outrun every other tetra, and none of them can catch it.

Tetra-1, as the fastest tetra, will never appear on the menu of any tetra, including its own. For one thing that rapidly emerges from predator calculations is that it is never worthwhile for any tetra to pursue its own kind, quite simply because other individuals of its kind can flee as fast as it pursues. If tetra-1 appears on nobody's menu, nobody appears on the menu of tetra-6, the slowest tetra. Tetra-6, or whichever is the slowest extant tetra, is perforce a grazer.

The speed differential between the idlest grazer - tetra-2.5 - and the fastest predator - tetra-1 - opens the possibility that tetra-2.5 populations, which generate the final extinction in Figure 17, might be restricted, and the tetra system endure longer.

Figure 19

Figure 19 shows the result when the same initial populations and range of tetras as shown in Figure 17 are used, but the tetras are omnivores instead of grazers.

The striking feature of this family tree is the frequent periods of population stability. For quite long periods, populations remain almost static, particularly in the range of smaller grazers, which hitherto tended to multiply to extinction. In these cases, each tetra population tends to be predators of the next smallest population. Thus tetra-3 eats tetra-3.5, which eats tetra-4, which eats tetra-4.5, and so on. The stable populations tend to contain larger numbers the smaller the tetra. During the periods of population stability, the tetras in the chain are generally not full-time predators, but alternate between predation and grazing.

The stable populations arise where predators exist in sufficient numbers to actually reduce tetra populations, and do so to a threshold level where they have become sufficiently scarce for the omnivorous predators to revert to grazing. During the stable periods, tetra predators graze while target populations multiply through the threshold, and then re-adopt predation until the target population numbers have fallen back below the threshold, in a repeated duty cycle. If pasture energy densities are high, the predation threshold is high. As pasture energy density falls, the threshold falls. Thus when the grass thickens, the stable populations slowly rise, and as the grass thins, predation increases, and stable population levels fall.

At the outset in Figure 19, grazers evolve much along much the same lines as in Figure 17, with a rash of extinctions, because the predator populations are too small to hold down numbers, or because high pasture energy densities result in the omnivore tetras adopting a grazing option. Later, as populations of larger tetras grow, and pasture energy densities are kept fairly low, predators exist in sufficient numbers to prevent population explosions. However, although populations are roughly stable, they tend to be gradually rising, if only because the unpredated populations of larger tetras are rising exponentially. Thus the pasture energy density gradually falls, and a 'slow' Malthusian crisis develops. It's noticeable that, as the crisis gets under way, predation increases, as the tetras increasingly find predation a more attractive option than grazing. This doesn't suffice to reduce numbers enough to avert the full crisis, and the tetras begin to succumb in the usual order - the least idle first, and so on -.

Re-diversifications after extinctions are regularly characterised by an initial rash of extinctions. This is because smaller tetras re-evolve from populations of larger predator tetras which are insufficient in numbers to prevent population explosions. When these predator populations have reached a sufficient size, however, population explosions and subsequent Malthusian crises tend not to arise.

This doesn't seem to always be the case, though. The final long period of population stability in Figure 19 is interrupted by a single extinction event which is preceded by a population explosion among the smallest tetras, which appears to be caused by a reduction in the numbers of predators further up the chain, which in turn seems to have been caused by increased predator activity still further up. Thus the predator chains appear to have their own quite complex internal dynamics.

Despite the presence of predators, however, this run lasts no longer than the equivalent grazer system shown in Figure 17. While, in the final stages tetras in the range -3 to -5.5 have stable populations, tetra-2.5 numbers continue to steadily rise, indicating that its own predators are unable to hold down its numbers. The system ends, as before, when tetra-2.5 populations grow to the point where the pasture cannot support them, and they become extinct, followed shortly by their predators.

In this case, since the system was initialised with a small population of tetra-6s, it appears that there were simply never enough of the slowly reproducing tetra-2s and tetra-1.5s to hold down the population of the most efficient grazer - tetra-2.5 -.

Figure 20

Figure 20 shows the result where the system is initialised with a relatively large population of tetra-2s. The immediate result is diversification of both tetra-2.5s and tetra-1.5s. The small and slowly growing populations allow the pasture energy density to climb offscale. After a fairly long period of diversification towards smaller tetras, energy density comes down rapidly, and there is the usual rash of pre-stability extinctions. After stability is achieved, energy density begins a steady fall, and a 'slow' Malthusian crisis, which produces a set of widely spaced extinctions. The large tetra-2 population succeeds in restricting tetra-2.5 numbers, until (as a part-time grazer), at the depth of the trough of pasture energy density, it becomes extinct. And although it fairly rapidly re-evolves, it never manages to restrain the now-burgeoning population of tetra-2.5s. The system enjoys a relatively brief renewed period of stability before the excessive numbers of tetra-2.5s bring final extinction. The entire run lasted a little over twice as long as its predecessor, indicating that in this case the presence of predators of tetra-2.5 succeeded in deferring the final extinction.

In the final run shown in Figure 21, the system was seeded with a population of tetra-1.5s. Apart from a veritable bushfire of extinctions prior to stabilising, the story is much the same. After populations have stabilised, with energy density falling, a long series of extinctions gets under way, culminating in the extinction of tetra-1.5. The survivors of this extinction are the two most efficient grazers - tetra-2.5 and tetra-2 -, and two of their predators - tetra-1 and tetra-0.5 -. After this point, with a large population of tetra-2s, the final pattern is almost a straight repeat of the previous run shown in Figure 20. The run however, lasted 10 times longer than the original grazer-only model.

Figure 21

The longer the TETRA model runs, however, the longer it takes to get results. The run shown in Figure 21 took some 30-40 hours on an 33-MHz 80386 IBM PC.

The conclusions drawn from the TETRA models are that, with unrestricted population growth with an all-grazer range of tetras, Malthusian crises and extinctions tend to come thick and fast. If, however, a predator system can establish itself, it appears that populations can remain relatively stable for quite long periods. In this case, however, long term slow growth in the population brings a creeping Malthusian crisis and creeping extinctions, or else instabilities in the predator chain result in population explosions and more rapid extinction events.

The attempt, with the predator versions of the tetra model, was to see whether predation could hold down grazer populations, and avert the otherwise inevitable Malthusian crisis. And for long periods, the simple omnivorous predators of the TETRA model succeeded in doing exactly this. However, gradually rising predator populations and/or the complex dynamics of the predator chain produced fast or slow crises in the long run. The bigger picture that emerges from the TETRA model is thus something like punctuated equilibria. During the 'equilibrium' phase, which may be very long, predators hold down grazer numbers. The system, however, periodically breaks down, with 'punctuations' of mass extinctions.

The long run equilibrium phase would be far more complex than the TETRA model suggests, however. In the first place, real grazers would not be feeding on the non-diverse, uniform, photosynthetic mush of the TETRA model, but would be selectively choosing individual plant species, much as the predators would choose grazers. The result, assuming that grazers opt for the softest, most energy-rich plants, would be that hard (e.g. woody) plants, or plants covered in thorns, or plants with low energy contents, would gradually tend to predominate, because the grazers would tend to be cropping those which gave them the largest energy return for least energy expenditure (i.e. highest K), and leaving the rest. The grazers would, in the long run, therefore tend to generate a steadily more fibrous, thorny, unreachable, low calorie pasture for themselves. The plants themselves could be treated as organisms essentially no different from their grazers, some being more efficient and idler than others, and it may be at a cost to its own efficiency that a plant expends energy in forming protective thorns, spikes, poisons, and so forth.

And much the same as applies in grazer-grass interactions would apply in predator-prey interactions. A predator which is using speed to overtake its quarry is liable to select out the slowest variants of its target population, and thus to produce a population which can run faster and faster as the aeons of the predator equilibrium phase pass. As the target populations run faster, only those predators which can catch them will survive, and thus the predator population will itself be selected for increasing speed. However, it is unlikely that the long term trend towards increasing speed will produce a more efficient, idler grazer: a grazing animal is unlikely to be more successful as a grazer for having the ability to run at 40 mph. Thus the long term trend in the predator era is likely to be one of steadily decreasing idleness, since the increasingly inefficient grazers have to work longer at grazing. Equally, since the predators would have to expend larger amounts of energy in pursuit of their ever more fleet-footed quarry, predator K-values would decrease, and predator idleness would decrease. In short, as the predator era went on, life would get steadily harder for all concerned. Such falls in idleness could be sustained for a long time because of the relative abundance of vegetation in the predator era. But in the long run, I suggest, the system would break down. It would break down either when idleness fell to zero for either the predators or their prey, or when it became physiologically impossible for speeds to be further increased, as either the pursuer or the pursued reached the 'design limits' of their biological construction.

In much the same way, the predator era would tend to select for fast reproducers among the predated populations. A population of slow reproducers, whose numbers grew slowly if at all, would tend to find its numbers dwindling to extinction, as predation reduced the population faster than reproduction replaced losses, leaving only faster reproducers. Equally, if a predated population consists in a mix of individuals who begin reproducing at different ages, members which reproduce latest will have to evade predators longer than there earlier-maturing cousins, and thus those which reproduce earlier will have a greater chance of successfully reproducing, and the long-run tendency even in populations which are not under threat of predation extinction will be for faster reproducers to become steadily predominant. The long term trend must therefore be that reproduction rates gradually increase during the predator era. However, fast-reproducing organisms must necessarily devote comparatively more energy to expensive reproduction, and will be consequently be less efficient, and less idle. Thus the long-run trend of increasing fertility will be attended with gradually falling idleness. Equally, steadily climbing reproduction rates will result in a steadily increasing likelihood that predators will become unable to restrict populations. And the predators, of course, are having to work harder anyway to offset increased target population speed, armour, camouflage, zig-zagging, and so on. Somewhere down the line, something has to give.

If the predator era opens with adaptable omnivores, the increasing demands on predators will gradually force specialisation. The jack-of-all-trades omnivore will gradually become a professional full-time carnivore; herbivore traits and capabilities thrown overboard in the attempt to maximise speed, acceleration, and range. The full-time predator then becomes a specialist hunter rather than a general-purpose predator, some specialising in high speed pursuit, some in armour-piercing teeth, others in the capture of small game, others in larger quarry. The one-time omnivore with a balanced portfolio of shares in the meat and vegetable market ends up as majority shareholder in difficult beef. The exposure of these specialists to a market crash gradually becomes complete.

All the time, of course, idleness is falling. During the predator era, it is still the idlest which survive, but all concerned are gradually becoming less idle. If idleness for any species ever reached zero, it would forthwith become extinct. In a variant of the 'slow' Malthusian crisis of the TETRA model, instead of vegetation becoming thinner on the ground, the grazers became less efficient at collecting it. If a predated population was ever driven to extinction in this way, its specialist predators would follow immediately, if they could not turn their attentions elsewhere (and in so doing introducing an instability into the entire predation system). If the predators arrived at extinction first, however, their former prey would begin to multiply rapidly, and a general Malthusian crisis would emerge if other predators could not restrict their numbers.

As far as physiological 'design limits' are concerned, it would seem most likely that a predator would encounter this limit before its prey, because a predator must always maintain an overall advantage over its prey - in speed, in maneouvrability, or whatever -, and in doing so it must always tend to be nearer any physiological limit than its prey. If the prey can move at the same speed (or faster) than the predator, it will regularly escape, and predation will become impossible. Thus, with the onus on the predator to always be one step ahead, the predator is always required to go one better. If, or rather when, it fails, the predated population escapes, multiplies, and the Malthusian crisis get under way.

And even if predators always kept one step ahead, and idleness stayed at viable levels, the long run of the predator era would produce populations of such inefficient grazers and predators that even the mildest of Malthusian crises would be liable to produce a firestorm of extinctions among them.

The Mesozoic heavily-armoured ankylosaurs - described sometimes as the "tanks" of the era -, the multi-horned and helmetted ceratopsians, and their tyrannosaur predators were the product of just such a long predation era, and none of them survived the terminal firestorm. In a Malthusian crisis, heavy armour, helmets, horns and spikes, are just so much impedimenta; useless weight to be lugged around in the increasingly labour-intensive stages of a Malthusian crisis. Camouflage, erratic zig-zag motion, the ability to run at 50 mph and reproduce like crazy, are no assets either in a Malthusian crisis in which high grazing efficiency, minimal cost overheads, slow reproduction, and maximum idleness are the indispensable keys to survival.

A zip file - tetra.zip holds the MS Quickbasic 4.5 source code and some input (.IN) files which give initial populations, and .DAT files which contain tetra characteristics. SIM11 was designed to run over long periods intermittently, saving its data in a restart file. The output file contains populations of variously sized tetras and grass energy density. The time periods used are variable, increasing when not much is happening, and decreasing when things get complicated.

cfd nov 98