Idle Theory employs a little simple physics. Most of this is concerned with the physical concepts of Work and Energy.

Work is done when a force is moved through a distance. When a mass of 0.5 kilograms is raised 2 metres against the gravitational acceleration of the earth (9.81 m/s²), 0.5 x 9.81 x 2.0, or 9.81 Joules of energy is used. (Work and Energy are interchangable terms.)

The potential energy of this mass is 9.81 Joules. If it is released and allowed to fall back, its velocity, v, after falling 2 metres will will be 4 x 9.81 m/s, and its kinetic energy will be 1/2.m.v² = 9.81 Joules. Thus its potential energy will have been converted into kinetic energy - energy is conserved.

Quantity	Equivalent	Dimensions	S.I. units
Mass		M	Kilogram (kg)
Length		L	Metre (m)
Time		T	Second (s)
Frequency	cycles/unit time	T-1	Hertz (Hz)
Area	length x width	L2	m2
Volume	length x height x width	L3	m3
Density	Mass/unit volume	ML-3	kg/m3
Velocity	Distance/unit time	LT-1	m/s
Acceleration	Velocity/unit time	LT-2	m/s2
Force	mass x acceleration	MLT-2	Newton
Weight	mass x gravitational acceleration (terrestrial surface acceleration = 9.81 m/s2 = g)	MLT-2	Kilogram (?)
Pressure or Stress	force/unit area	ML-1T-2	Pascal (Pa)
Moment of Inertia	mass x length2	ML2	kg m2
Work	force x distance	ML2T-2	Joule (J)
Energy	Work capacity	ML2T-2	Joule (J)
Potential Energy	mass x gravitational acceleration x height raised	ML2T-2	Joule (J)
Kinetic Energy	1/2 mass x velocity2	ML2T-2	Joule (J)
Power	Work/unit time	ML2T-3	Watt (W)
Momentum	Mass x velocity	MLT-1

The S.I. (or M.K.S.) system has the kilogram as its unit of mass, not weight. At the surface of the earth, a kilogram weighs 9.81 Newtons.

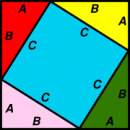
Theorem of Pythagoras

A small square is drawn inside a larger square such that its vertices touch the sides of the larger square. The area of the larger square can be expressed in two ways. 1) Area = (a + b)2 = a2 + 2.a.b + b2 2) Area = c2 + 2.a.b When areas 1) and 2) are equated 3) a2 + b2 = c2 This is my own proof, first posted on the web 2 April 1998 (ftp file edit date). I'd probably first thought of it in about 1991, after I saw an interesting proof by re-arrangement discovered in Egypt. When I first went searching for this proof on the web in 1997, I couldn't find it. Which is why I posted up what seemed to me to me a related but then-unknown proof. I was very surprised to find it rather prominent on Wikipedia some 10 years later, as the 'algebraic proof' of Pythagoras. Perhaps it was already known. But several features of the Wikipedia algebraic proof suggest that it was derived from my proof. Firstly the notation is the same, and so also is the diagram used, as also is coloration of the diagram -although they use different colours (shown right). I called this proof 'the method of two squares', but the Wikipedia name, the 'algebraic proof' is perhaps more accurate, in that this proof requires the use of algebra. However, allowing for this, it seemed to me to be one of the simplest proofs around. In what way does one decide that one proof of Pythagoras is "better" than another?

Equations of Rectilinear Motion
1) v = u + a.t	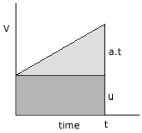where u = initial velocity v = final velocity a = acceleration t = time s = distance
2) s = u.t + 1/2.a.t2 (s is area under graph)
3) v2 = u2 + 2.a.s (combining 1) and 2))

Newton's Laws of Motion

First Law of Motion: Every object continues in its state of rest or uniform motion in a straight line unless a net external force acts on it to change that state.

Second Law of Motion: The rate of change of momentum of an object is directly proportional to the force applied and takes place in the direction of the force. This becomes force = mass x acceleration, p= m.a

Third Law of Motion: To every action there is always an equal and opposite reaction.

The Laws of Thermodynamics

Zeroth Law: Suppose that of three bodies A, B, and C, bodies A and B are separately in thermal equilibrium with body C, then bodies A and B are in thermal equilibrium with each other. This permits temperature measurement.

First Law: The change in internal energy of a system is equal to the the heat absorbed by the system plus the external work done on the system. This is a statement the conservation of energy. Energy is neither created nor destroyed.

Second Law: For an isolated system, only those processes can take place for which the entropy of the sytem increases or remains constant. Clausius' statement of the Second Law: It is impossible to construct a device that operating in a cycle will produce no effect other than the transfer of heat from a cooler to a hotter body. The spontaneous flow of heat from a colder body to a hotter body is impossible. Lord Kelvin and Max Planck's statement of the Second Law: It is impossible to construct a device operating in a cycle for the sole purpose of extracting heat from a reservoir and changing it into an equal amount of work without rejecting a part of the heat. i.e. it is impossible to devise a machine that converts 100% of heat into work. The universe is cooling down.

Third Law: It is impossible to reach the absolute zero of temperature in any physical process.

Potential and Kinetic energy From Newton's second law, force = mass times acceleration. So at the surface of the Earth, where gravitational acceleration is g, a mass m has a force (also known as 'weight') exerted on it given by p = m.g The work done, W, moving a force through a distance equals force times distance. And if force p is raised a height h, the work done W in raising this mass - also known as potential energy P.E. - is: P.E. = W = p.h = m.g.h If this mass, with initial velocity u = 0 is released and allowed to fall under gravitational acceleration through height h, then from equation 3 of rectilinear motion, its velocity v after falling that distance is given by v2 = u2 + 2.g.h Since u = 0, this can be rewritten as h = v2 / 2.g Substituting h into m.g.h gives kinetic energy K.E. P.E. = m.g.h = m.g.v2 / 2.g = K.E. and K.E. = m.v2 / 2

Newton's law of gravity:

F = G . M₁ . M₂ / R²

where F is the gravitational force, G is the gravitational constant, M₁ and M₂ are two masses, and R is the distance between them.

Centrifugal or centripetal force:

F = M . R . W²

where M is a mass revolving at radius R from an axis with angular velocity W.

Bayes' Theorem

References:

Introductory College Physics. Atam P. Arya. Collier Macmillan.