Stream-fed Populations

The S-Curve

But as from the the high geometrical powers of increase of all organic beings, each area is fully stocked with inhabitants, it follows that as each selected and favoured form increases in number, so will the less favoured forms decrease and become rare. Rarity , as geology tells us, is the precursor to extinction. (Darwin. Origin Ch.4 emphasis added)

Perhaps the standard model of population growth is the S-curve, also known as the Logistic Equation. According to this, population rises to a maximum value, called the carrying capacity, K. It might then be said, as Darwin put it, to be "fully stocked."

The Logistic equation seems to have appeared ex nihilo. It is attributed to Verhulst (1838) and was later adopted by Pearl. It has been subjected to regular attack. But there are examples of populations which grow in this way. For example, bacteria grown in chemostats behave in this fashion. In a chemostat, a constant flow of nutrients is fed into one end of a tank containing bacteria, while the same volume is removed at the other end.

A simple simulation model of a chemostat isn't very difficult to produce. A population of animals grazes in a stream of passing nutrients. Each animal has a basic metabolic rate of energy consumption, and an energy cost of movement from one location to an adjacent one, and a constant rate of energy expenditure for reproduction - so that each animal reproduces at a constant rate. To offset these energy expenditures, the animals gain energy by eating the nutrients which steadily flow in. If the animals ever run out of energy, they die, and are removed from the stream.

In the chemostat simulation model, the creatures start out dispersed in the stream, but fairly rapidly, as their numbers rise, move towards the right hand side where the nutrients are being fed in. The small initial population of creatures multiplies, but soon stabilizes at a more or less constant level. Thus the simulated chemostat behaves much like the real apparatus. And it demonstrates S-curve population growth.

This model tends to develop regular peaks at the reproduction interval of the grazers. If grazers reproduce at the highest nutrient density, their offspring are more likely to survive. The largest subpopulation, when it doubles in size, tends to create a nutrient famine shortly after, and so subpopulations that reproduce during this famine are unlikely to prosper. The result is that while at the outset reproduction is randomly distributed, it ends up concentrated at one point in time.

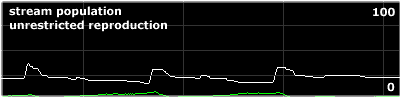simulation

One way to produce a more stable population is to have the creatures to occasionally delay reproduction. If starvation inhibits reproduction, this will act to distribute reproduction more evenly, and to prevent concentration at one particular time.

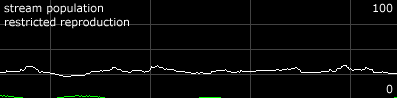simulation

The reason that the population stabilizes is fairly straightforward. With the population dispersed along the right hand edge, most of the nutrients flowing in are immediately consumed, leaving little or nothing for any creatures downstream. Any creature which moves very far downstream is thus likely to die, unable to find enough nutrients to sustain it. The carrying capacity of the stream is the total energy flowing into the stream divided by the sum of each creature's metabolic, reproductive, and movement energy expenditures.

One interesting consequence of this , which the simulation model can demonstrate, is that the stream carrying capacity rises as reproduction rate falls. This is because slow reproducers expend less energy on reproduction, and consequently more of them can be kept alive by a given nutrient energy flow into the stream

Also, if reproduction rates are allowed to vary, such that the offspring of any one creature has some equal chance of reproducing a little faster or a little slower, the simulation model regularly shows reproduction rates rising. The explanation of this is again fairly simple. Dispersed evenly along the right hand side, the creatures each have an equal chance of getting food. They are each as likely as any other to stay alive. Thus those that reproduce fastest tend to predominate.

Another notable feature of this simulation is that, with all the creatures arranged in a line at the right hand edge, there is the likelihood of direct competition between them for food as it flows in. As they jostle together, it is easy to see that the strongest or the fastest is most likely to get food than slower, weaker creatures. In fact, in these simulations, the creatures simply take turns to feed, and none are faster or stronger than others, nor take priority over them. One simple measure of contention is to count the number of creatures which are in the same grid square at the same time, and this measure shows regular contention, particularly just after a burst of reproduction.

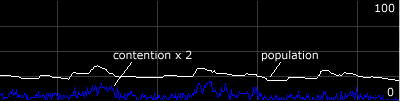The interest of this is that it shows how the idea of tooth-and-claw competition might have arisen. These creatures, arranged along the right hand edge, can be compared with farm animals feeding at a trough, wedged together, pushing and shoving, the weakest thrust aside or trampled underfoot by the strongest.

The face of Nature may be compared to a yielding surface, with ten thousand sharp wedges packed close together and driven inwards by incessant blows, sometimes one wedge being struck, and then another with greater force. (Darwin. Origin Ch.3)

In total, this simulation demonstrates

1. S-curve growth to carrying capacity, the Darwinian view.
2. Natural selection for rapid reproduction.
3. The likelihood of direct competition for food.

Review

Although this simulation demonstrates the Darwinian scheme where populations multiply and compete for scarce food resources, there are several reasons for supposing that it may not accurately reflect the realities of natural life.

Plants which are powered by the stream of radiation from the sun are clearly living in a nutrient stream. And plant populations typically rise to a stable level. Organisms that live in rivers, and feed on material flowing downstream, might also be considered to live in a nutrient stream. The same might apply to coral reefs which feed from current-born nutrients. Where a population rises to a stable level, and the creatures tend to stay in one place, the best guess is that they feed from a stream of nutrients of some sort.

But, for plants, the stream of energy from the sun is not constant, but cyclical. In the first place there is the cycle of day and night, and in the second place there is there is the cycle of seasons, with solar radiation at a minimum in winter, and at a maximum in summer. If the energy flow into the stream simulation is changed from constant to slowly cyclically varying between a minimum and a maximum, the stream population rises and falls with this cycle. Furthermore, if the amplitude of the cycle is sufficiently great, the simulation shows that instead of fast reproducers coming to predominate, slow reproducers come to predominate. And the reason is simple: at some low level of energy inflow, energy- expensive fast reproducers are unable to survive, where energy-conserving slow reproducers can. Fast reproducers are gas-guzzlers, and they need an energy-rich environment. This selection for slow reproducers may explain plant succession where the climax state where the slowest-growing plants (like oak trees) predominate over fast-growing plants (like grasses).

Another objection must be that plant populations are regularly subjected to the predations of grazing animals of every kind. This must act to reduce plant populations below their potential maximum.

But the principal objection to the stream model of population growth must be that not all living creatures live in nutrient streams. Most terrestrial animals, grazers or predators, do not live in a stream of energy. For a grazing animal, the population of plants on which it feeds represents a pool of nutrient energy, not a stream. A population of grazing animals can, in principle, consume all the plants available in their pool. Solar-stream-feeding plants can never do this with radiation from the sun. Pool feeders rapidly exhaust the nutrients in their locality, and consequently need to be able to move around relatively rapidly to find more. Grazing cattle feed faster than the grass beneath their feet can grow. If they did not, they would never need to stir from the place on which they stood.

Conclusion

S-curve growth to carrying capacity occurs in nature in stream-fed populations, such as plants. Direct competition is relatively intense and continuous. Selection favours fast reproducers in some circumstances, slow reproducers in others.

It's notable that, in Origin, a great many of Darwin's examples are of plant life. And also many of the experiments Darwin describes were carried out with plants. The idea that an area would become "fully stocked" with inhabitants was most likely drawn from observing plants.