Pool-fed Populations

Plants gain their energy from the solar radiation stream. For grazing or browsing animals, a plant population is a pool of energy.

The simulation model of stream populations can be used, with slight modifications, to model pool populations. Instead of nutrients streaming across the field of grazers, they are scattered evenly over the field, in the form of growing plants on which grazing animals may feed. The same overall amount of nutrients are added each day to the pool as are added to the stream. The plants grow to a maximum size. The grazers disperse across the field.

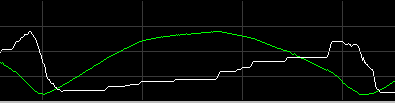
Whereas a stream-fed population rises to a near-stable level, the pool-fed population oscillates. As the grazers multiply, they reduce the level of nutrients in the field to the point where they can no longer survive. In a short period, most of them die, leaving only a few lucky survivors - and occasionally no survivors at all. Largely ungrazed, the nutrient grass regrows, and the small population of surviving grazers begins to multiply, until they again overgraze the field, and another population crash occurs.

simulation

In a stable pool-fed population, grazer idleness is constant at some intermediate level. In the pool-fed population, average idleness is high while grass density is high, but falls rapidly as grass density dwindles to a low level, and the grazers find it increasingly hard to find food.

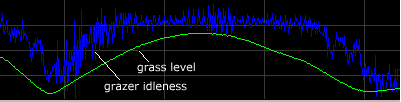With the creatures dispersed across the field, there is little or no contention between them. Some contention appears as population reaches its maximum - unlike in stream-fed populations where contention is intense and near continuous. The explanation in part lies in the fact that nutrients are dispersed in a field, but are concentrated as they flow into a stream. The more nutrients are concentrated at particular locations, the more direct competition results, as grazers collect at these locations.

If grazer reproduction rate is allowed to vary, so that the offspring of a grazer has a 50% chance of reproducing either more rapidly or slowly, this simulation selects for low reproduction. The reason is simple. When population crashes, gas-guzzling fast reproducers are more likely to run out of fuel, and die, than their less energy-expensive slow reproducing cousins. In this simulation ever more slow-reproducing grazers emerge from each crisis, some of them non-reproducers. The cycle takes longer and longer, and the maximum population grows ever higher.

Ultimately, in this simulation model, a population consisting entirely of non-reproducers is liable to appear in the aftermath of one of the population crashes. This population would remain stable (because these grazers don't age), and the grass density would remains high and stable. The non-reproducers would live largely idle lives in a stable environment. But the introduction of a single predator, even a very inefficient one, would result in their rapid extinction.

If the grazers stop reproducing when starving, then the population initially rises as before, and then falls abruptly when grass levels have fallen to a low level. But population then stabilizes, with grass at a low level, and the grazers working hard to stay alive.

simulation

In this case, a small increase in the level of grass results in increases grazer reproduction which reduces the grass level, and hence eradicates the increase in population. The grazers are kept at starvation levels.

If grazer reproduction rates are allowed to vary as before, the slower reproducers again gradually predominate. This is because they are able to survive at lower grass densities. In this simulation, the stable population level gradually rises as reproduction slows, and the grass level falls. Yet, as reproduction rates fall, and population rises, population stability is lost, and oscillation recommences.

This stability only arises if the starvation level at which grazers stop reproducing is set relatively high. If the starvation level is set lower, the simulation shows the population oscillating again. Clearly the reproduction constraint has to come in early if stability is to be achieved, and also earlier for slower reproducers than fast reproducers.

If seasonal change is imposed, so that grass growth rates cycle around a mean level, the simulation shows population level cycling slightly behind the seasonal cycle.

Conclusion

Pool-fed populations tend to oscillate in numbers. There is little direct competition. And selection favours slow reproducers. Population stability can be achieved if individual grazers shut down reproduction when starving.