The idle cell model provides a primitive entity which consumes energy, grows, and reproduces by binary fission. Beginning with a single cell, at division there will be 2 cells, and at the next division 4 cells, and then 8, and so on. If the unit of time is taken to be the life cycle of the cell through division-growth-division, then the birthrate, B, is one cell/unit time, and the population after time, T, after growth from some initial population at time 0, is given by:

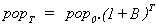
No natural death-rate is assumed here, since the cell model offers no account of natural ageing and death. If a natural death rate, D, was to be included, the population after time T would be given by:

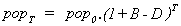
Assuming that the availability of energy in the environment remains stable, the population of cells will grow exponentially indefinitely.

For the purpose of this discussion, populations are regarded as populations of cells dispersed in a pool in which energy ( in the form of solar radiation for plants, and in the form of chemical energy in sugars and fats and proteins for grazers ) is also evenly dispersed at some concentration which is termed the energy density. It is taken that plant cells capture solar radiation, and use this energy to produce sugars, starches, and proteins. The population of plant cells is itself evenly dispersed because the sun shines equally at every place. Those grazing animals which feed upon sugars and starches and proteins of plants are presented with an evenly dispersed field of plants, and these grazers are evenly dispersed across that field. And again, where predators feed upon grazers, their prey are again found to be evenly distributed. And it is assumed that where plants or grazers are consumed, that the resulting local fall in energy density, as it appears to grazers and predators, is rapidly made up, as plants and grazers continually mix and disperse. This is, of course, a simplification. The earth is of course spherical, and the intensity of solar radiation is at a peak at the equator, and at a minimum at the poles, and therefore plant life is presented with a steadily falling energy density as it approaches the poles. Again, the rotation of the earth results in the solar power available to plants being switched on for half the day, and off for the other half. And the tilt of the axis of rotation of the earth results in annual seasonal cycle of solar energy density at any point on the surface. Rather than attempt to introduce these various complications, the simplest circumstance is considered: the sun shines evenly upon the surface of the pool. In a pool in which numerous unicellular organisms are dispersed, the assumption of even distribution appears reasonable. On land, where plants are rooted in fixed locations, there is no sense in which the loss of one plant results in the others all shuffling over to restore an even distribution. But if grazing land animals are dispersed among plants, then it can be taken that plants are being consumed at equal rates across the terrain, and that seedlings are everywhere springing up to fill the cleared areas. Nevertheless, soil conditions, variations in altitude are bound to make for an uneven distribution, with higher energy densities at one place than another, the plants growing more densely at one location than at another. But the essential assertion is that regardless of the sphericity and rotation and tilt of the earth, and the partition of its surface into land and sea, and the variation in the height and composition of the land surface, the constant tendency is towards even field distribution of energy resources rather than their point concentration.

Pool feeders:

If a population of cells is seen as reproducing in a closed pool of limited size in which nutrient energy is evenly distributed by constant mixing, the growing population of cells will gradually draw down the nutrient concentration - or energy density -. As this happens, the extractors will have to work harder to induct energy into the cell, and their idleness will fall. At some point, the pool energy density will fall to the point where cell extractor idleness reaches zero, and ZID ensues. If the environmental energy density is even throughout the pool, and all cell extractors operate at the same idleness, all cells will die simultaneously, and the cell population fall to zero, while pool energy density remains at whatever level ZID occurred.

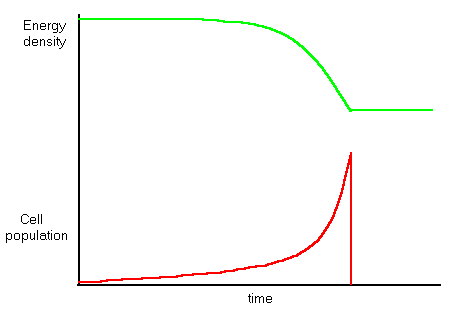
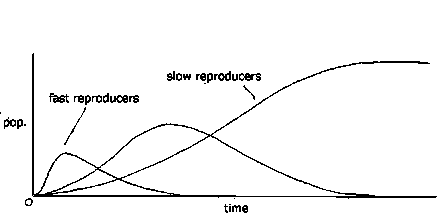
If the initial population is made up several different cell types with different reproduction rates, then as the population rises, the faster-reproducing cells, which are less idle than slower reproducers, arrive earlier at zero idleness death. The population peaks as the fast reproducers die off, and dwindles away as the smaller population of slower reproducers is gradually removed.

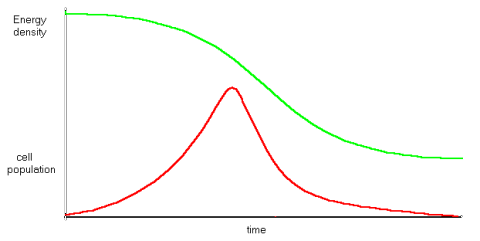
The point here is that reproducing cells are operating at less than equilibrium idleness, doing more work than is necessary to simply maintain themselves. This means that both assemblers and extractors are less idle than those in a cell which is simply maintaining itself. As pool energy density drops, the idleness of all cells fall, and the fastest reproducers reach zero idleness, and death, before slower reproducers. It follows that non-reproducers will survive the longest of all, although even a tiny population of these will slowly reduce the energy density of the pool. There can be different variants of the pool. The pool may be having nutrients added to it. To a population of grazing animals, vegetation represents a pool of energy, which they deplete by consuming, but which recovers as plants grow.

Flow feeders:

Another variant situation is where cells are multiplying along a stream of nutrients. As each cell removes nutrients from the stream, the energy density is fractionally reduced, so that downstream cells are progressively less idle, and a point is reached on the stream where the energy density is so low that cells cannot survive.

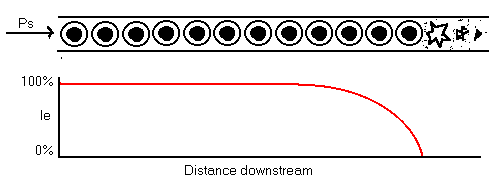
If it is assumed that the cells reproduce along the length of the stream, in a column, and (for simplicity) that each cell draws the same power, Pu, from the stream, then given the power input at the head of the stream is Ps, the number of cells that can be supported is roughly:

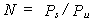
From a single cell, the population will multiply exponentially along the stream until there are N cells. Beyond this level, continuing reproduction will result in the excess population over the first N cells dying in the downstream region. The population will thus rise to a maximum stable level.

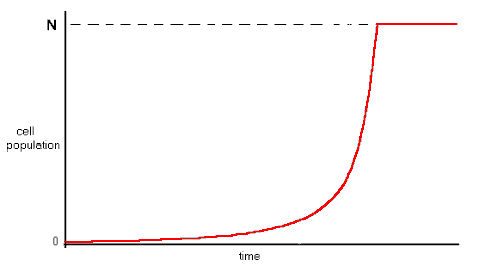
Pu, the power usage of individual cells along the stream, is lower for slow-reproducing cells than for more active fast-reproducing cells. Thus the maximum population in the stream, N, is higher for slow reproducers than fast reproducers. Another consequence is that while slow-reproducing cells reach higher maximum populations, there is a smaller flow of dead cells into the downstream region. By contrast, while fast-reproducing cells in a stream attain lower maximum populations, there is larger flow of dead cells into the downstream region.

Given a small mixed initial population of fast and slow-reproducing cells in a stream, the faster reproducers will rapidly colonize the stream, and the resulting population will mostly be comprised of fast reproducers. At least, at first. However, since it is always possible for a sub-population of slow reproducers to survive downstream of the last fast reproducer, a sub-population of slow reproducers will appear in the downstream region, pushing up the proportion of slow reproducers. If, over time, the fast and slow reproducer populations mix in equal proportions along the stream, fast reproducers will gradually become outnumbered and finally replaced by slow reproducers.

If several differentially reproducing populations are introduced into such a stream, the fastest reproducers reach peak populations in succession, each one dwindling thereafter in numbers, with the slowest reproducer eventually reaching a stable population.

This is strongly analogous to terrestrial plant succession, where waste ground is first colonized by fast-growing grasses and shrubs, followed by bushes, small trees, and finally by a climax population of mature oak. Terrestrial plants, which receive their energy from the stream of radiation from the sun, can indeed be regarded as stream feeders. Their populations can be expected to rise to a stable maximum, and mixed populations to pass through a succession until a single slow-growing species survives. Also, if the model applies, fast-growing grasses can be expected to provide an abundant downstream supply of dead vegetation, in layers beneath them. And it does appear that prairie grasslands build up deep layers of soil, and that thinner soil layers are found beneath forests. If the flow of dead plant matter into the soil provides a source of energy to power a population of decomposers, the soil itself could be regarded as a stream that supported a climax population of decomposers. Beneath prairies, there could be expected to be a large decomposer populations, but much lower populations beneath forests.

The two simple models of population - in pools and streams - demonstrate two kinds of population behaviour. Pool populations boom and crash. Stream populations grow to a climax population level. The only difference between the various kinds of cell considered here lies in their reproduction rate, which is determined, perhaps, by the relative length of non-coding regions in their assembler control loops. Fast reproducers have short lengths, slow reproducers long ones. Intuitively, it might be expected that the fastest reproducers would simply rapidly outnumber their slower reproducing counterparts, and become the dominant 'species.' But in both pools and streams, while fast reproducers do initially greatly outnumber their fellows, in the long run it is the slowest reproducers which survive past the demise of the fast reproducers.

Plants and grazers:

If stream feeders correspond to plant life, growing and reproducing in the stream of radiant energy from the sun, and pool feeders correspond to animals which feed on pools of energy - such as the energy stored in plants -, then the two can be combined into a model where grazing animals feed on a plant population.

These plant eaters may have arisen from soil decomposers which feed off the flow of dead material downstream from a plant population. The decomposers would have to have the ability to recover energy from dead plant material. Plant succession, however, acts to gradually convert a fast-reproducing plant population, with a large flow of dead plant matter downstream, to a slow-reproducing population with a small flow of dead matter. As far as plant decomposers are concerned, this change means a fall in the energy input into their stream, and a fall in idleness, and dwindling populations. This may have forced a shift in the strategy of some decomposers, from eating dead plant material to killing and consuming live plants. This could have been a gradual process. The decomposer stream is immediately downstream of the plant stream. The original decomposers would simply have lived off the excess plant matter shed by the plant stream, and not attacked the living plants. One simple reason for this may be that a live plant cell, unlike a dead one, can repair itself, and a decomposer that (metaphorically) set out to apply its can-opener to a live cell would find that the can resealed itself as soon as it was opened. Decomposers would simply have to work harder to break down living cells than dead ones. In an environment rich in dead plant cells from a fast-reproducing plant population, large decomposer populations could be maintained. But as plant succession proceeded, and the supply of dead plant matter dwindled, and decomposers became less and less idle, and their populations fall, the extra cost of attacking abundant live plant cells would gradually be offset by the rising cost of finding dead plant cells. For the decomposers, it would be a choice between living off easy-to-eat but increasingly scarce dead cells, and living off hard-to-eat but increasingly abundant live plant cells. At some point the balance would tilt in favour of plant predation rather than plant scavenging. The first true herbivores would appear. And for the them, the climax plant population would appear as a huge pool of hitherto untapped energy. This shift in strategy would begin among the less idle decomposers, most threatened by the dwindling supply of dead plant cells. The most idle decomposers would tend to find the balance still favoured continuing scavenging.

Once the scavenging decomposers turn plant predators -grazers -, they multiply in the plant pool. As with any pool feeder, the growth in their population decreases the energy density in the pool, in this case thinning out the plants. In a closed pool, energy density is drawn down to the point where pool feeders can no longer survive. However, with a reproducing plant population, plants removed by grazers are being replaced by new plants, and initially a small grazer population removes plants at a lower rate than plant reproduction replaces them, and the plant population remains at climax. But as the grazer population grows exponentially, it gradually starts eating plants at a rate faster than plants reproduce, and the plant population begins to fall, and grazer idleness begins to fall as plants become harder to find. The least idle grazer types - the fastest reproducers - meet with extinction, and a series of extinctions decimates the grazer population. At each extinction, a grazer sub-population is removed, and total plant consumption by grazers slows. At some point, the population of grazers falls to a point where plant growth outstrips grazer predation, and the plant population begins to recover, and returns to climax. The relatively small number of slow-reproducing grazers then gradually multiplies and repeats the whole process.

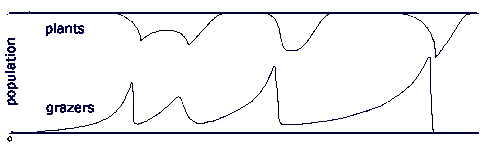
Here there are a fixed number of grazer types, and the series of extinction removes first the fastest reproducers, followed by the slower reproducers, until the final extinction removes the slowest reproducers. If, however, variation is introduced, such that periodically one of the grazer types give rise to a variant which reproduces more rapidly or less rapidly, the result is that the series of extinctions continues, so long as there is always a small sub-population of slow-reproducers. At each extinction, the least idle, fast-reproducing populations are removed. In this simple evolutionary model, several sets of grazers multiply until their combined numbers pull down the energy density of the plant population, and decrease grazer idleness. There follows a rash of extinctions as the least idle grazers reach zero idleness. These extinctions reduce grazer impact on plants, and allow plant populations to recover, and grazer idleness to rise again. A cycle is set up where long periods grazers idleness are interrupted by relatively brief crises where idleness falls as plant populations collapse, and some grazer lines become extinct.

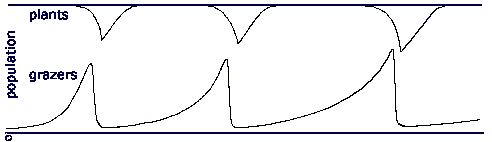
If it is taken that variations are rare, then the greatest variation is likely to arise when populations are large. This means that, in this cycle, most of the variants will appear towards the end of the cycle, as the extinction crisis approaches, and the largest sub-populations throw up numbers of variants. By contrast, there would be few variants appearing in the small post-crisis grazer population. Thus for most of the cycle, the grazers would retain the same distribution of types. A tree of the various types would show the extinctions as terminations of lineages along distinct lines, with a few lines surviving, and diversifying into new variant lineages.

The effect of grazers upon the plant population is to reverse the natural succession process. As grazers remove plants, the slowest reproducing plants - the climax plants - replace themselves very slowly, and faster growing plants appear in the plant stream. Thus the effect of the grazer predations is to reduce the numbers of slow-growing plants, and increase the proportion of fast-growing plants. Under prolonged and intensive grazer predation, slow-growing plants will become rare, and the fastest-growing plants will gradually predominate. 13

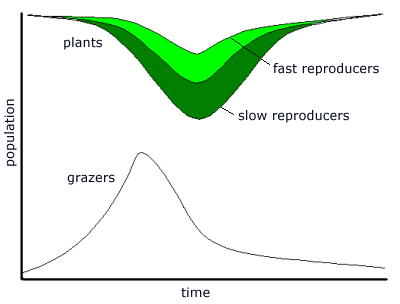
After a series of extinctions has decimated the grazer population, normal plant succession will resume, with slow-reproducing plants gradually becoming predominant at the next plant climax. Fast-growing plants will become rare again. Thus, left to themselves, without any grazers, plants will self-select for the slowest reproducers. Under predation, they will be selected for the fastest reproducers. Thus there are two mechanisms: one to decrease reproduction rates, the other to increase it

Predators:

The explanation offered for the appearance of grazers has been that, at plant climax, when large and mostly slow-reproducing plant populations predominate, the downstream detritus feeders, which live off a flow of dead plant cells from the living plant population, find that the energy flowing to them is steadily diminishing, and they are becoming less idle, and some of them switch from scarce dead plant cells to a diet of abundant live plant cells. Thus detritus feeders become plant grazers. The same explanation can be offered for the appearance of predators who consume grazers rather than plants. As a population of grazers gradually multiplies, and plant populations begin to fall, grazers become less idle. A point arrives where, as grazers multiply, and plants are decimated, that some of the less idle grazers find that they increase idleness if they switch from eating plants to eating grazers. Quite simply, the growing number of grazers provides a growing pool of energy, available for consumption. So while the most idle grazers continue with a diet of plants, some of the least idle grazers switch to a diet of grazers. The switch need not be sudden. At first, as plant populations fall, and the energy density of the plant pool drops, the least idle grazers begin to die, and their remains provide a source of energy for scavengers. These scavengers, rather like the detritus feeders downstream of the live plant population, simply feed on dead grazers in addition to plants. The step from scavenging to predation is then simply a shift from consuming dead grazers to capturing and consuming live ones. This can be assumed to be more difficult, as live grazers attempt to escape. Extra energy has to be expended by a predator in capturing and killing a grazer, over and above the energy expenditure of eating a dead grazer. However, if there are enough live grazers, this extra cost will be offset by the sheer numbers of grazers available to such a predator. The option is between living off an limited supply of easily consumed food, or an abundant supply of less easily consumed food. As relative numbers of plants and grazers change, some grazers may switch from grazing to scavenging and predation, and then back to grazing, simply adopting whatever strategy maximizes idleness. It's a two-way track. However, an omnivore that can switch from predation to grazing is not likely to be the best grazer or the best predator - just fairly good at both. If it's assumed that a good predator needs to be able to move faster than its prey, then there must be an energy cost in maintaining long, powerful legs - or whatever is needed to achieve high speed. High speed doesn't help grazing, however, because plants don't run away, and so for a grazer long and powerful legs are a liability, not an asset. The tendency must regularly be for omnivores to remain dedicated grazers, or become dedicated, full-time predators. The grazer population, to full-time predators, has the same relation as the plant population to grazers. Multiplying predators are likely to decimate the grazer population, reducing the energy density of the grazer pool, and decreasing predator idleness. The least idle predators will succumb to the increasing difficulty. Only the most idle predators will survive when grazers have been decimated. As predators reduce grazer populations, they also act to reduce pressure on plant populations, so that a decrease in the number of grazers allows plant populations to recover. When, however, overpredation of grazers brings a slump in predator populations, grazers begin to multiply again, and plant populations come under renewed pressure. The result is that as predators increase in numbers, grazers decrease in numbers, and plant populations tend to rise. As predators decrease, grazers increase, and plant populations tend to fall.

The result may be an oscillating, dynamic stability, with plant and grazer and predator populations remaining stable over long periods. However, just as grazers act to increase plant reproduction rates, predators also act to increase grazer reproduction rates. Left to themselves, grazers will tend to self-select for low reproduction. When predators appear, they can be assumed to impose the same death rate on both fast and slow reproducing grazers alike. For fast reproducing grazers, this death rate may be less than their reproduction rate, and so their numbers will rise. For slow reproducers, the same death rate may exceed their reproduction rate, with the result that their numbers fall. Predators thus act to generate a population of fast reproducing grazers. Increasing plant and grazer reproduction rates mean falling plant and grazer idleness, as more effort is devoted to reproduction. At the same time, it can be expected that grazers will tend to eat those plants which are not fortuitously protected by being tough, fibrous, or armed with thorns and spines and poisons. The result will be that, as defenceless plants are removed by grazers, the remainder are increasingly well defended. The grazers have to work harder to overcome these defences, and their idleness falls as a result. Equally, since the surviving plants have to perform extra work in maintaining defences, plant idleness also falls. The same applies to the relation of grazers and predators. Predators, by catching the slowest or least defended grazers, gradually create a population of increasingly fast-moving or heavily armoured grazers. The grazers, of course, have to perform extra work maintaining armour, or high speed legs. Their idleness falls. As does the idleness of the pursuing predators.

The long run effect of this 'arms race' is steadily falling idleness for all living entities. Plants become tough and thorny and poisonous. Grazers develop heavier and heavier armour. Predators become steadily more powerful. There must be an increasing tendency for grazers to become specialists at eating one or other particular kind of well-defended plant, and for predators to concentrate upon particular well-armoured grazers. Specialist grazers and predators emerge, which concentrate their attacks on one target, whose defences other grazers and predators are unable to overcome. And the result of falling idleness is a slow series of extinctions, as one or other predator or grazer type reaches zero idleness. Given a high degree of specialization, each plant may have one single dedicated grazer, and this grazer a dedicated predator. In fact there could be a whole string or chain of entities, each feeding upon the next, and a number of sets of such chains.

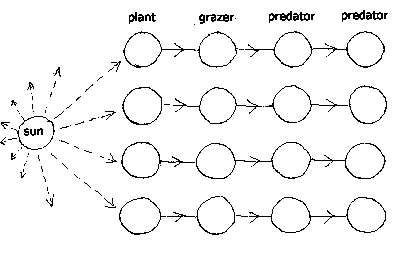
The extinction of one entity in this chain would result in the rapid extinction of all the entities dependent upon it. The entity on which it depended, now freed from predation, would begin to freely multiply in numbers. If this was some type of plant, it would become abundant, regardless of its natural reproduction rate, because other plants would continue to be subject to the attention of their dedicated grazers. A kind of succession would ensue where plants which no extant grazer could eat would gradually predominate, and other plants become rare, reducing their dedicated grazer idleness, and producing another wave of extinctions. The final situation would be one where only a few grazers and their predators remained, and most plants would not be attacked by grazers. At this point, another plant succession would emerge, in which plants which could increase their idleness by ridding themselves of their burdensome defences - spines, thorns, poisons - would come to predominate. Heavily armoured plants would become rare. And the remaining grazers could then extend their diet to encompass a wider range of undefended plants. Grazer idleness would increase.

Extinction and diversification:

Two kinds of long term cycle have been offered here. In the first, there are only plants and grazers, and grazer populations boom and crash, cyclically. In the second, predators hold grazer populations in check, and populations remain roughly stable, but with steadily falling idleness as both plants and grazers develop ever stronger defences against attack, and falling idleness ultimately results in a series of extinctions. Both these cycles involve a period where grazers initially enjoy an idle life amid a profusion of plants. This idle life gives way to one of increasing toil as either the plants become scarce, or develop defensive mechanisms. During the easy time, grazing animals multiply and diversify freely. As life becomes difficult, the least idle variants meet with extinction, and only the most idle survive into the next cycle where plants are again profuse and undefended, and grazer populations low. In the easy time, most new variants appear, because the high energy density in the plant pool allows improbable variants a better chance of success. When times get hard, and plant energy densities are falling, new variants have less chance of surviving. This is also a view of the natural world which sees no 'balance of nature,' but instead a dynamic process of continual change.

This simple cyclic scheme of evolution would appear to operate quite well over relatively short periods of time - a few centuries or millennia - and provide a steadily chugging evolutionary engine. But it appears to be rather harder to use it to explain global extinctions such as those at the end of the Permian and Cretaceous periods. For assuming that the surface of the planet is broken up into distinct localities - seas, lakes, islands, continents - which are largely independent of each other, cycles of variation and extinction could be expected to be in different phases in different places. The only ways of explaining global extinctions using this kind of evolutionary cycle is

1) To suppose that periodically, quite by chance, different localities come into phase together. Thus extinctions occur in localities X, Y, and Z, not because they are causally related to each other, but simply because they happen to coincide. Sooner or later, it's bound to happen.