
|
The IdleLife applet shows the populations of 40 different varieties of reproducing creatures. The population levels oscillate up and down as the creatures overgraze the pool in which they feed, and then recover their numbers. The model shows the formation of 'species islands', as least idle intermediates become extinct. |
The IdleLife simulation model has 40 different varieties of creature feeding from a nutrient pool which has a constant input of new nutrients. The nutrient density in the pool is not homogeneous. There are 9 regions, with nutrient densities ranging from below average to above average. The creatures are assumed to be dispersed equally among the 9 sub-pools.
The creatures differ in two ways. Their maintenance power, Pm, expenditure varies with the sine of their index number (0 -39), and also falls slightly with index. Pm is a falling sine wave. At the same time their reproduction power expenditure also falls linearly with index number, so creatures with low index numbers reproduce faster than creatures with high index numbers. Creatures with the highest index numbers have generally got lower Pm values that creatures with low index numbers.
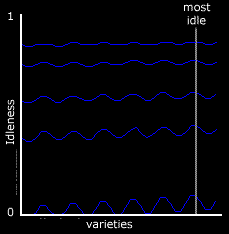 When the pool is rich in nutrients, or (same thing) the pool
energy density is high, the creatures are largely idle, and
idleness tends to fall into a high, narrow range. But as
energy density falls, they become less idle, and at the same
time differences in idleness become more apparent. The graph
on the left shows this effect for the different varieties of
creatures in the simulation: as idleness falls, the underlying
sine wave becomes more apparent. At the lowest level, the idleness
of some varieties is zero, and these varieties die. Thus as
energy density falls, and idleness falls, some varieties
- or some subpopulations of them - die out.
When the pool is rich in nutrients, or (same thing) the pool
energy density is high, the creatures are largely idle, and
idleness tends to fall into a high, narrow range. But as
energy density falls, they become less idle, and at the same
time differences in idleness become more apparent. The graph
on the left shows this effect for the different varieties of
creatures in the simulation: as idleness falls, the underlying
sine wave becomes more apparent. At the lowest level, the idleness
of some varieties is zero, and these varieties die. Thus as
energy density falls, and idleness falls, some varieties
- or some subpopulations of them - die out.
With initially rising populations, more nutrient energy is removed from the pool than is being fed into it, and pool energy density falls, and some of the subpopulations in the pool die, reducing overall population. When populations have been reduced sufficiently, more energy is entering the pool than is being consumed by the remaining population, and pool energy density rises, and idleness also rises. A repeat cycle is set up.
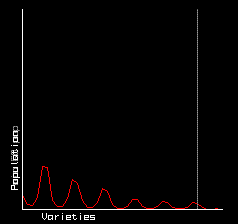
|

|
| Populations shortly after start of simulation. | Population at end of simulation. |
When seeded with an initial small population, at first all the creatures multiply, the busy low index ones faster than the idle high index ones. But fairly rapidly they reduce the nutrient density in the pool, and their populations collapse, then recover, and collapse again.
But a pattern soon emerges. The creatures with the lowest Pm values - the most idle - gradually predominate. A series of islands (created by the underlying sine wave function) emerges. Intermediates between the islands first become rare, then extinct.
Although low index varieties reproduce faster, it is the high index varieties, which reproduce slower, which gradually predominate. Little by little, the islands dwindle and vanish, leaving only the most idle variety, its population oscillating up and down.
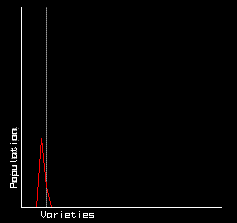 In the foregoing example, the creatures only die when the pool
energy density falls to levels at which they cannot survive.
But if some fraction of the population is regularly killed off by
some other agency - predation, or accidents, or disease - the
result is quite different.
In this 'predation' scenario, the fastest reproducers tend to
predominate - or at least the most idle fast reproducers.
In the end, one island population of fast reproducers remains.
If predation death rates are too high, the entire population
is driven to extinction by the predation toll.
In the foregoing example, the creatures only die when the pool
energy density falls to levels at which they cannot survive.
But if some fraction of the population is regularly killed off by
some other agency - predation, or accidents, or disease - the
result is quite different.
In this 'predation' scenario, the fastest reproducers tend to
predominate - or at least the most idle fast reproducers.
In the end, one island population of fast reproducers remains.
If predation death rates are too high, the entire population
is driven to extinction by the predation toll.
 If the fraction of creatures being killed is reduced, two
populations can coexist. One is the fast reproducer that
survives heavy predation. The other is the most idle slow
reproducer, which survives zero predation.
If the fraction of creatures being killed is reduced, two
populations can coexist. One is the fast reproducer that
survives heavy predation. The other is the most idle slow
reproducer, which survives zero predation.
These two populations tend to vary with respect to each other. Sometimes there is more of one, sometimes more of the other.
Other related models show quite complex population behaviour, with several different varieties coexisting over long periods, but their relative populations shifting around, so that at one time any one of them may outnumber the others. One explanation for this is that where a slowly reproducing population is reduced to a low level, other faster reproducing populations may quickly overtake it in numbers, only to be themselves reduced as the slowly reproducing population recovers its numbers.
These simulations demonstrate how an initially even distribution of different varieties of creatures can become concentrated into islands, which might be thought of as 'species' separated by a sea of missing intermediate types. This kind of 'speciation' occurs without geographical isolation, from an initially diverse population from which the least idle drop out.
They also demonstrate a form of 'succession', where an initial diversity of types progresses to a climax state where only one or two varieties remain.
These simulations are built using the Idle Life physical model. Source code is available.
