Idle Theory's economic simulation model was written before I started to think analytically. The simulation models were mathematically extremely simple. But when I had some results from the simulations, I wondered if they were right, and whether there was some way of checking. Thinking analytically, coming from another direction, I began to piece together a few equations. I used these equations to compare with the simulation model results. They agreed. Here are some of them:

Humans have always had to work to survive. As hunters, they have had to hunt, kill, and eat animals. As gatherers, they have to find, collect, and eat plants. This work is necessary work, in that if it is not done, humans will starve and die.

A useful tool is something that saves more work time than it costs to make it. For example, in a hunting society, a flint knife that takes 1 hour to make may reduce the daily time taken to dismember animals from two hours per day to one hour per day - a saving of one hour per day. If the flint knife lasts a week before it breaks, then it will produce a net saving of 7 hours of work over its lifetime, for the expenditure of one hour of work spent making it.

In Idle Theory, the 7 hours saved is termed the value of the tool, and the one hour spent making it is termed its cost. Something is a useful tool if its value is greater than its cost, and the use of such tools results in increased idleness, where idleness is the fraction of time that the tool user is idle, or not engaged in necessary work. If value is less than cost, then it is a luxury, or a useless article.

The process of making and using such tools can be described graphically over time. Given some initial level of idleness, the work done making the tool first may be represented as a fall in idleness, and the consequent savings in work time can be represented as a rise in idleness. The cost and value of the tool is represented by the areas of decreased and increased idleness.

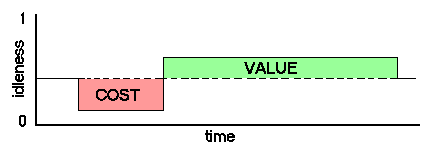
The above graphic is only one of many possible tool cost-value diagrams. Some tools may not break, but gradually become 'blunter' and less useful over time. The value of edible crops lies in their nutrient value, and future continued life time that this provides. But the cost of producing such crops is largely determined by the time it takes them to grow from seed.

Some tools may also save time in making tools. Someone who makes flint knives and axes may use special implements to strike the flint. These implements in turn need time to make or find.

It should be noted that with very low values of initial idleness, where individuals have very little idle time, the cost of making tools may need to be spread over a longer period. And at extremely low levels of idleness, it may be entirely impossible to make tools.

Equally, at very high levels of idleness, the value of tools must tend to decrease, because there is very little work time to be saved.

Calculating Idleness

For the most part, in the following calculations, it is taken that all members of society are physically identical, and have exactly the same requirements and capabilities (except perhaps of skill). It is also taken that they are as physically active in their idle time as they are when busy working. This is a simplification. But the following equations are only intended to be indicative of a simple circumstance.

In the absence of any useful tools, where individuals only have their bare hands and feet to perform work, everyday life will have an untooled idleness, I_U. This value may be somewhere between 0 and 1. But it may also, on occasion, be less than 0 - which is to say that without tools individuals will be unable to survive.

Where V reperesents tool value, and C represents tool cost, and L is tool lifetime (the duration of its period of use), then the net rate of saving of work time, or the net increase in idleness dI, that results from regularly making and using such a tool, is given by:

dI = (V - C)/ L

And if someone has a whole set of such tools, used independently of each other (e.g. one tool saving time in one activity, another tool in some other activity), then given N tools the resulting increase in idleness is given by the sum of the the increases of idleness they each provide:

dI = S^N₁ (V_n - C_n)/ L_n

The resulting actual idleness is the untooled idleness, I_U, plus the increase in idleness.

I = I_U + dI

The increase in idleness resulting in using such tools cannot, of course, increase idleness above complete or unit idleness.

Trading Societies

In some circumstances, individuals make make and use their own tools, and live entirely independently of other people. But in many human societies, a division of labour arises, whereby each person has a particular task to do, and may specialize in making one particular tool. So, in a society which uses flint knives and axes, one or two people may make all the knives and axes used in that society. This may happen because some people are naturally better at making them, and either produce better knives, or produce them more quickly, or both. The products of such people will have lower costs and higher values. Furthermore, as they grow skilled over time, they are likely to be able to produce higher value knives at lower and lower costs. If it takes most people 3 hours to make a flint knife that only has a value of 4 hours, but one skilled individual can make the same flint knife in 10 minutes, it is best if this individual make knives for everyone else.

The same circumstance may arise where one human society that is highly skilled in making useful flint knives and axes encounters a society which is highly skilled in making useful whicker baskets, and both wish to own and use each other's tools.

In both circumstances, it will be likely that such tools will come to be traded - one thing given in exchange for the other. And since the fundamental costs and values of these tools are measured in time, the price at which they exchange must also be fundamentally measured in time. And so the price of any tool will be some amount of time. The buyer of a tool will offer to work on behalf of the seller for some period of time, and they will bargain over the price until they agree upon it. And after many such bargainings, the price is likely to settle upon some fixed amount. After all, such bargaining is itself a form of work, and fixing a price removes the cost of bargaining.

At what price are tools likely to be exchanged? In the first place it may immediately be said that if the agreed price is the cost of the tool, then the toolmaker is merely compensated for his efforts, and gains nothing from the exchange. If the price is less, he loses time. Equally, if the price is set at the value of the tool, then the buyer gains nothing from the exchange. And if the price is higher than the value of the tool, he will lose time.

But given that, with useful tools, the value is always higher than the cost, there is a range of prices, between cost and value, at which both buyer and seller both gain time from the exchange. And there must also be a price at which both buyer and seller gain exactly equally. And so, price will usually fall somewhere between cost and value.

Various factors may act to push prices either down towards costs, or up towards values. In the case where various manufacturers compete to supply the same tool, prices are likely to be driven downwards as manufacturers seek to undercut competitors and gain market share. In the case where tool manufacturers cannot meet demand, prices are likely to be bid upward by buyers. Equally, in the absence of competition, monopoly manufacturers may be able sustain high prices.

Analysis of a Simple Trading System

In one simple economy or trading system, it may be imagined that some number of individuals each make and sell a useful tool of one sort or other, and there are as many tools, N, as there are individuals. If the prices of these tools are P₁, P₂, P₃, P₄, etc, and evey member of the trading system buys a new tool as soon as it needs replacing, then given tool lifetimes L₁, L₂, L₃, L₄, etc, each member will spend at a rate given by

rate of expenditure = P₁/L₁ + P₂/L₂ + P₃/L₃ + P₄/L₄...

and so

rate of expenditure = S^N₁ P_n/L_n

And at the same time, given that N individuals are each buying every tool, each tool manufacturer, n, will have an income given by

income = N . P_n/L_n

The result, taking each manufacturer in turn, will be that net income for manufacturer n will be given by

Net income = N . P_n/L_n - S^N₁ P_n/L_n

Given a trading system with 3 members ( N = 3 ) the net incomes of each are:

Net income(1) = N . P₁/L₁ - S^N₁ P_n/L_n
Net income(2) = N . P₂/L₂ - S^N₁ P_n/L_n
Net income(3) = N . P₃/L₃ - S^N₁ P_n/L_n

A positive net income will mean that a member will be buying labour, and a negative net income will mean that a member will be selling labour.

And where total net income is the sum of the individual net incomes,

Total net income = N . S^N₁ P_n/L_n - N . S^N₁ P_n/L_n = 0

A total net income of zero means that the trading system will neither gain nor lose money.

And the resulting increase in idleness of each member will be given by

dI_n = net rate of time gained from using tools - net rate of time spent manufacturing tools + net income.

or, where V_n/L_n is the rate at which time is gained through tool n use, and C_n/L_n is the rate at which time is spent making a single tool n,

dI_n = S^N₁ V_n/L_n - N . C_n/L_n + N . P_n/L_n - S^N₁ P_n/L_n

And, where I_U is untooled idleness, or individual idleness in the absence of any tools, the actual idleness of individual members, I_n, is untooled idleness + increased idleness:

I_n = I_U + dI_n

Given most possible sets of prices, the idleness of individual members, I_n, are unlikely to unlikely to be equal. Some people will be more idle than others.

Values of I_n need not necessarily fall between 0 and 1. Where I_n < 0, this will correspond to the death of member n. Where I_n > 1, this will correspond to a circumstance where member n is completely idle, and has one or more other members working for him.

Just Prices

The 'just price' (a mediaeval and scholastic notion) of tools may be regarded as the set of prices which result in equal idleness across the trading society. Such a set of prices may be calculated by setting individual idleness equal to the mean idleness of the trading system. The mean idleness of the system is simply untooled idleness plus the increase in idleness accruing from using all tools:

I_mean = I_U + S^N₁ (V_n - C_n)/ L_n

And, where N = 3, setting individual idleness, I_n, equal to mean idleness gives a set of 3 equations:

I_mean = I_U + S^N₁ V_n/L_n - N . C₁/L₁ + N . P₁/L₁ - S^N₁ P_n/L_n
I_mean = I_U + S^N₁ V_n/L_n - N . C₂/L₂ + N . P₂/L₂ - S^N₁ P_n/L_n
I_mean = I_U + S^N₁ V_n/L_n - N . C₃/L₃ + N . P₃/L₃ - S^N₁ P_n/L_n

Subtracting the first equation from the second equation results in

P₂/L₂ - C₂/L₂ - P₁/L₁ + C₁/L₁ = 0

or P₂ = C₂ - ( P₁ - C₁ ) . L₂/L₁

or more generally,

P_b = C_b - ( P_a - C_a ) . L_b/L_a

Repeating this process across the whole trading system results in a set of just prices which will result in a general equality of idleness among all members of the trading system. And it may be noted that if P_a = C_a, then P_b = C_b, and one set of just prices is where tools are traded at their costs.

In general, in a trading system in which manufacturers compete to sell tools, prices will be pushed down towards costs, and the net result will be an approximate equality of idleness across society.

Unjust Prices

Just as it is possible for a set of just prices to be calculated, which result in an equality of idleness among members of the trading system, so also it is possible to calculate unjust prices. Unjust prices (or perhaps 'most unjust' prices) are a set of prices whereby all the gains in idleness in the trading system accrue to a single individual, such that everyone else is continually working (at zero idleness) for that individual. If the single individual is member 1 then the set of equations required to find these prices, where N = 3, is:

3 . I_mean = I_U + S^N₁ V_n/L_n - N . C₁/L₁ + N . P₁/L₁ - S^N₁ P_n/L_n
0 = I_U + S^N₁ V_n/L_n - N . C₂/L₂ + N . P₂/L₂ - S^N₁ P_n/L_n
0 = I_U + S^N₁ V_n/L_n - N . C₃/L₃ + N . P₃/L₃ - S^N₁ P_n/L_n

In such perfectly unjust societies, it may be thought that individuals can simply 'drop out' of the tool trading system with its unjust prices, and live an untooled existence. However, they can only do this if untooled idleness, I_U, is greater than zero. If I_U is less than zero, then dropping out results in death. In this circumstance an individual faces a choice of either staying in the trading system, working continuously, or dropping out and dying. Given such a choice, he is effectively locked in.

Such unjust systems are also termed 'dragon economies', and are likely produced by monopoly production of tools.

It may well be that, historically, the religious institution of the sabbath, where nobody worked for one day in a week, or two weeks, arose as a safeguard against the eventuality of people working continuously all their lives. If so, such sabbaths were intended to provide a minimum level of idleness, not a maximum. And in circumstances where social idleness fell below that sabbatical minimum, work would have had to be done on the sabbath.