
In this essay a simple model of walking is used to estimate the power consumption at different walking speeds. The results are then compared and fitted to published figures from empirical studies.
Humans move up and down as they walk, and the approach taken here is to suppose that most of the work being done in walking is in raising the body mass between paces. The rate at which humans walk forward is regarded as being determined by the length of strides taken and the natural swing period of legs, regarded as compound pendulums.
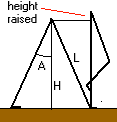 When someone with leg length L takes a pace forward, their legs are at an angle 2A to each other. In taking the next pace, one leg becomes upright as the other leg swings past it. The result is that with each pace taken, the body must be raised from a height H above ground level to a height L above ground level, or L.( 1 - cosA), and the work done w.d. in raising body mass m through this height is
When someone with leg length L takes a pace forward, their legs are at an angle 2A to each other. In taking the next pace, one leg becomes upright as the other leg swings past it. The result is that with each pace taken, the body must be raised from a height H above ground level to a height L above ground level, or L.( 1 - cosA), and the work done w.d. in raising body mass m through this height is
w.d. = m.g.L(1 - cosA)
If the swinging legs are treated as rod pendulums [1], their swing period (assuming small angle A - at larger angles period is greater[5]) is given by
T = 2.pi. sqrt( 2.L/3.g )
So the mechanical work rate is the work done per pace in raising the body mass divided by half the leg swing period T. Given a leg length of 1 metre, the leg swing period is 1.64 seconds, so the period of swinging one leg forward in taking a pace forward is about 0.82 seconds. The swing period is assumed to stay the same regardless of swing angle A. Kinetic energy of forward motion is assumed constant.
Given the pace length is 2.L.sinA, forward speed of motion is pace length / half leg swing period. when A is about 13 degrees, pace length is about 0.45 m, and forward speed is about 2 km/hr.

|
| Fig 1. Mechanical workrate against speed. 50 kg body mass. 1 m. leg |
If body mass is 50 kg, the work done per pace is 50 . g . 0.025 or 12.25 J and given pace time 0.82 s, this works out as 15 J/s or 15 watts at 2 km/hr.
At 5 km/hr, mechanical workrate rises to 106 watts (see graph at right). At 0 km/hr, the mechanical workrate is zero.
While work is done lifting body mass during walking, this mass is lowered in each step cycle, and some fraction of the potential energy released in falling may be stored in leg muscles, which act like springs. This stored energy is used when body mass is raised, reducing the amount of work that has to be done.
Like any engine, the human engine is inefficient. Only part of the energy stored in the body as sugars and fats is converted into mechanical work, while the rest is lost as heat. The thermal efficiency of many engines is in the range of 20-30%. If the same applies to humans, the actual rate at which stored energy in the human body is mobilised will be 3 to 5 times the mechanical work rate.
Comparison with empirical data
Graph 1 shows the mechanical work rate, m, required to walk on flat ground at various speeds. Mechanical work, m, is also multiplied by a factor, f, to represent how much mechanical work is stored in muscle 'springs'. Given a basal metabolic rate, b, and the inverse of thermal efficiency, e, net power consumption is assumed to be given by
E = b + e . f . m ------(2)
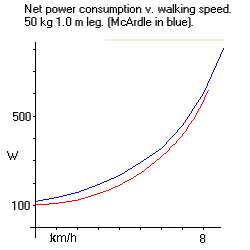
The upward-sloping curve shape is also found in studies by McArdle et al of human power consumption while walking on flat ground. By judicious manipulation of b, e, and f in equation 2, an attempt was made to match these figures.
A fairly good match was obtained with body mass 50 kg, leg length 1.0 m, and b = 100 W, e = 3.333 (corresponding to a 30% thermal efficiency) and f = 0.4 (indicating that 60% of mechanical energy is stored in muscles for release later in the stride). The comparison is shown in Fig 2. A value of b of 100 W corresponds well with a bmr of about 50 W/m^2 and DuBois skin surface area of 2 m^2. A thermal efficiency of 30% is comparable to many internal combustion engines. Whether a figure of 60% of mechanical energy being stored in muscle springs is plausible or not is left open. This 'best fit' is one that tries to balance plausibility with accuracy. Better fits are obtained with higher thermal efficiency than 30%.
McArdle also tabulates predicted values of power consumption for various body masses and walking speeds. Table 1 below shows predicted values (McArdle's in red). Predicted power consumption rises faster with walking speed than McArdle's figures, and rises slower with body mass than McArdle.
| ||||||||||||||||||||||||||||||||||||||||
| Table 1. Predicted power consumption (watts) for different body masses and walking speeds. McArdle's figures in red. | ||||||||||||||||||||||||||||||||||||||||
Other published figures [6] give heat production by someone walking at 2 km/h as 110 W/m^2 with body area of 1.8 m^2 (total 200W), and walking at 5 km/h as 200 W/m^2 (total 360W). The comparable figures here, for a 50 kg body mass and 1.0 m leg length are about 120 W and 240 W. So these figures differ from McArdle by a factor of 2. But no figures are supplied for the mass or leg length of the people in these studies. McArdle doesn't seem to give this either.
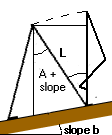 When someone is walking uphill, instead of the body mass being raised by (L - LcosA) it must now be raised by (L - Lcos(a + b)) where b is the slope angle. The height raised is greater, and so more work is done in raising the body mass. Conversely going downhill, the body mass must be raised (L - Lcos(a - b)), which is a smaller height, and so less work is done.
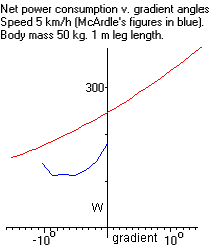
McArdle gives some figures for power consumption walking downhill. These don't compare very well with the results obtained in the present study (see Fig 3), where the mechanical work rate does indeed fall with steepening downslope, and reaches zero when A stride half-angle equals the downslope angle. Beyond this point, it is not clear what might happen. Someone walking down a slope may topple and fall if they don't increase their stride angle. Or they may have to perform work to prevent themselves from accelerating downhill. The uptick in the workrate of McArdle's results suggests that participants in his study were doing the latter. In the present study, it is assumed that no work is done when downslope angle exceeds stride half-angle.
When someone is walking uphill, instead of the body mass being raised by (L - LcosA) it must now be raised by (L - Lcos(a + b)) where b is the slope angle. The height raised is greater, and so more work is done in raising the body mass. Conversely going downhill, the body mass must be raised (L - Lcos(a - b)), which is a smaller height, and so less work is done.
McArdle gives some figures for power consumption walking downhill. These don't compare very well with the results obtained in the present study (see Fig 3), where the mechanical work rate does indeed fall with steepening downslope, and reaches zero when A stride half-angle equals the downslope angle. Beyond this point, it is not clear what might happen. Someone walking down a slope may topple and fall if they don't increase their stride angle. Or they may have to perform work to prevent themselves from accelerating downhill. The uptick in the workrate of McArdle's results suggests that participants in his study were doing the latter. In the present study, it is assumed that no work is done when downslope angle exceeds stride half-angle.
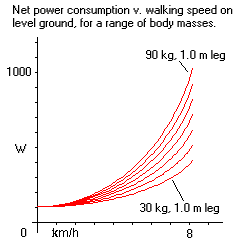
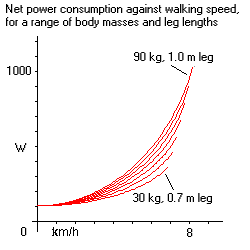
Also shown in Fig 4 is how power output varies with walking speed for body masses ranging from 30 kg to 90 kg. Fig 5 shows the same results for for a range of body masses and leg lengths, from 30 kg children with 0.7 m legs, to 90 kg adults with 1.0 m legs. Increasing body mass entails increasing mechanical work needing to be performed. Increasing leg length results in a reduction in mechanical work. The ideal walker is light and long-legged.
|
|
| Fig 2 | Fig 3 |
|
|
| Fig 4 | Fig 5 |
In addition, according to Wikipedia (quoted below) only 15% of food energy gets converted into mechanical work. It is assumed that the rest is turned into heat.
The conversion efficiency of food energy into physical power depends on the form of energy source (type of food) and on the type of physical energy usage (e.g. which muscles are used, whether the muscle is used aerobically or anaerobically). In general, the efficiency of muscles is rather low, and roughly speaking, only about 15% of the food energy is actually converted into mechanical energy. For example, when calculating food energy burnt per unit time gym equipment manufacturers multiply the value of physical power by a factor of eight (assuming 12.5% efficiency). Thus if an exercise bike registers a 150-watt physical power output it might display 17 kcal/min as the rate of food energy burnt per unit time (since 150 W x 8 = 1200 W or 17 kcal/min). (Wikipedia)
By 'food energy' is meant the calorific value of food before it is consumed. The human digestive system is also inefficient, and not all the energy in foods is extracted and stored in the body as sugars and fats. Since a mechanical efficieny of 30% is being assumed for the human body, a 50% digestive efficiency would result in overall food energy conversion efficiency of 0.3 x 0.5 or 15%.
Conclusions
The simple approach taken in this essay seems to produce walking power consumption figures that are of the right order of magnitude, compared with published figures. In general, the method seems to produce a rate of growth of power consumption with walking speed that is rather higher than published figures.
References:
1. Hyperphysics - Rod pendulum
2. Exercise Physiology McArdle et al.
3. Studies on the Mechanical Efficiency of Human Movement, Kihachi Ishii, 1982.
4. External, Internal, and Total Work during human locomotion
5. Physicslab pendulum physlet
6. Metabolic rates for common activities
7. Clothing, Activity, and Human Metabolism
8. More texts
9. Thermal Efficiency of a Human Being
10. Katch-McArdle formula based on lean body mass:

(kCal [1 KCal 4.185 kJ]) where LBM is the lean body mass in kg. According to this formula, if the woman in the example has a body fat percentage of 30%, her BMR would be 1263 kcal per day. (For example, a 55 year old woman weighing 130 lb (59 kg) and 5 feet 6 inches (168 cm) tall would have a BMR of 1272 kcal per day or 53 kcal/h (61.3 watts).) Calculate your body fat and LBM.
